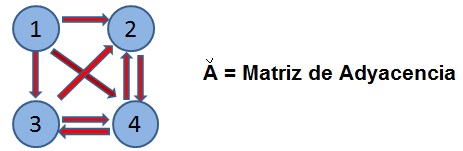Taller gratuito sobre Big Data y Deep Learning

MT Trading - NT2 Labs

Bienvenido al Taller Gratuito sobre los Fundamentos de Big Data y Deep Learning..
En este Taller usted tendrá acceso a los fundamentos de Big Data y Deep Learning, incluyendo específicamente los siguientes temas: Algoritmo de PageRank, Reglas de Asociación, Redes Neuronales Artificiales (Artificial Neural Networks), Red Neuronal de Aprendizaje Profundo y Mapas Autoorganizados de Kohonen.,

Inversión de tiempo requerido para este Taller: 3 horas de estudio más una hora para resolver el Cuestionario (4 horas en total).

Al finalizar el Taller y si usted lo desea, podrá obtener un certificado verificado de aprobación por un valor de USD 90 y extendido por MT Trading.

Inscríbase en el curso profesional sobre Big Data y Deep Learning, con una duración total de 24 horas, un valor de USD 370 y gestionado por MT Trading.

PASOS A SEGUIR

Paso 1: Bienvenida Paso 2: Conceptos previos sobre Big Data Paso 3: Algoritmo de PageRank Paso 4: Reglas de Asociación Paso 5: Redes Neuronales Profundas Paso 6: Cómo construir una Red Neuronal Profunda Paso 7: Mapas Autoorganizados de Kohonen Paso 8: Cierre Paso 9: Cuestionario Software de Deep Learning Paso 10: Si desea un certificado verificado y emitido por MT Trading: i) Envíenos sus respuestas al Cuestionario | Click aquí ii) Si consigue un mínimo de 70% de respuestas correctas, le envíaremos el certificado impreso por medio de Correos de Chile (valor: USD 90).

PASO 1: Video de Bienvenida - Ing. María José Olivares, NT2 Labs.

Importante En el curso completo de Big Data y Deep Learning, ya sea en su versión web (USD 210) o en la versión presencial (USD 370), se tratan muchísimos más temas y con el máximo detalle posible. De click aquí para solicitar mayores informaciones.

 

PARTE 1: Big Data
PASO 2: Conceptos previos sobre Big Data.
Big Data enfrenta cuatro grandes desafíos conocidos como Las Cuatro Vs. Estos desafíos son: velocidad, volumen, veracidad y variedad. En Big Data, los datos pueden estar agrupados en clusters y exhibir relaciones binarias. Por ejemplo, en un grafo cada nodo o vértice puede representar a un usuario de Facebook y la relación binaria puede ser “u y v son amigos”, con los valores posibles de 0 o 1. En este caso, la relación se representa con un enlace, arista o arco no direccionado, dado que si u es amigo de v, entonces v es amigo de u. Por otro lado, la relación puede ser direccionada o dirigida y debe representarse por medio de una flecha. Esto ocurre por ejemplo con la relación binaria “Followers” en Twitter. Es decir, el hecho de que u sea un seguidor de v no implica que v sea un seguidor de u.

Importante: Una relación binaria no direccionada se da en Facebook: Si el nodo X es amigo del nodo Y, entonces X e Y son amigos (no se necesita representar la relación con una flecha, si no con una línea). Por otro lado una relación binaria direccionada se da en Internet: Si el nodo o página web X tiene un link hacia el nodo o página Web Y, esto no implica que Y tenga un link hacia X.
La Matriz de Adyacencia "A" resume relaciones binarias y sus elementos A_ij son tales que:
A_ij = 0 si no hay relación entre los nodos i y j
A_ij = 1 si hay una relación que parte en el nodo j y termina en el nodo i (si hay una flecha desde j hacia i).

PASO 3: Algoritmo de PageRank (APR)
El APR es un algoritmo que permite definir el el nivel de importancia de una página web a partir de los links que apuntan hacia ésta, permitiendo de este modo ordenar los resultados de una búsqueda en Google desde la página más importante a la menos importante. La teoría está explicada en el paper de Larry Page y Sergei Brin del año 1998.

El ranking idealizado de los nodos de una red se puede asociar a la distribución de las probabilidades de visita que consigue un Random Surfer RS que navega por la red. Los métodos de navegación pueden ser:
i) Navegación sin taxation: el RS navega dando clicks en los enlaces presentes en cada página web.
ii) Navegación con taxation: se permite que el RS se teletransporte, ya sea escribiendo la dirección en la barra de direcciones o dando click en alguna de las páginas almacenadas en la barra de marcadores del Navegador. Al teletransporte se le suele asignar una probabilidad de 0.15.

Una Red o Net se puede representar con un grafo "G" como el siguiente:

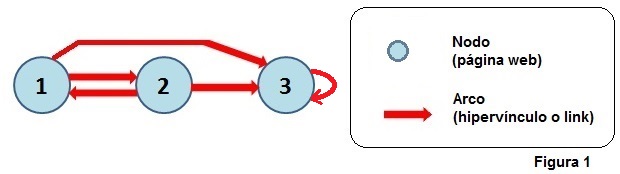
En el grafo se observa que:
- Hay un link de 1 a 2 y otro link de 1 a 3
- Hay un link de 2 a 1 y otro link de 2 a 3
- Hay un link de 3 a 3 ("self-loop")

El ranking de cada nodo se puede correlacionar con las probabilidades de cada nodo obtenidas por medio de un RS en el caso límite (cantidad de pasos ).

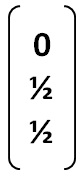
Por ejemplo, para el grafo G de la Figura 1, tendremos lo siguiente:

* Nodo 1 - Probabilidad de saltar a 1: 0 - Probabilidad de saltar a 2: 1/2 - Probabilidad de saltar a 3: 1/2 (El 2 del denominador es porque en total salen dos links del nodo 1) Resumen para el nodo 1:

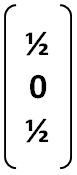
* Nodo 2 En total salen dos links del nodo 2. Resumen para el nodo 2:

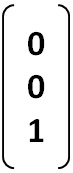
* Nodo 3 En total sale un link del nodo 3. Este link es un link interno (la página apunta a sí misma). Resumen para el nodo 3:

Luego, la Matriz de Transición de Markov "M" se construye con las tres columnas anteriores del siguiente modo:

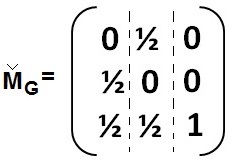
Dado que hay tres nodos, se tendrá que la distribución de probabilidades inicial del RS será:

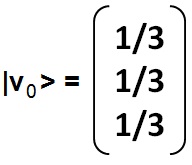
La distribución del RS después del paso n, y permitiendo teletransporte, se calculará con la siguiente igualdad (Page y Brin, 1998):
	Ecuación n°1

Siendo d la probabilidad de navegar dando clicks en los links de cada página (valor cercano a 0.85).

Para el primer paso del RS (n=1), obtendremos el siguiente vector de estado:

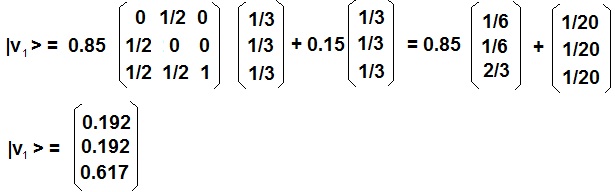
Es decir, el ranking o distribución de probabilidades después del primer paso será:
- Para la primera página web: 0.192
- Para la segunda página web: 0.192
- Para la tercera página web: 0.617

Como ya se mencionó, el ranking final se obtiene con .

Importante: Relación entre PageRank y Deep Learning
El PageRank de una neurona en un circuito o Red Neuronal Biológica (BNN) se correlaciona fuertemente con la probabildad de que esa neurona presente actividad, dado que la corriente electroquímica equivale a un Random Surfer viajando por las conexiones neuronales (paper de Jack McKay Fletcher y Thomas Wennekers del año 2017 ).

Conceptos Avanzados * El vector de estado en el paso n se obtiene por medio de la multiplicación del vector de estado en el paso n-1 con la matriz M, dado que sin teletransporte y permitiendo self-loop se tendrá que: Prob(saltar al nodo 3) = Prob(1 a 3)*Prob(de partir en 1) + Prob(2 a 3)*Prob(de partir en 2) + Prob(3 a 3)*Prob(de partir en 3). Claramente se está multiplicando una fila por una columna (Markov, 1907). * El ranking final (n tendiendo a infinito) se obtiene por medio del autovector de M correspondiente al autovalor lambda igual a uno. * En Internet existen páginas web con millones de visitas diarias vs otras con unas pocas visitas al día. Es por ello que en la práctica el ranking se expresa por medio de una escala logarítmica.

 

PASO 4 : Reglas de Asociación
Modelo de la Cesta de Supermercado
Imaginemos una venta o transacción en un supermercado identificada por el número de la factura. En la factura o transacción t_i se puede ver el detalle de la venta correspondiente a un subconjunto de todos los ítems i_j que vende el supermercado. Por ejemplo, la transacción t₁₀ puede tener como detalle al conjunto {i₄₀, i₁₀₇,i₉₀₃,i₁₀₇₂ } .

Definiciones
i) I: conjunto formado por la lista de todos los ítems i_j disponibles, con j de 1 a D.
ii) T: conjunto formado por todas las transacciones t_j realizadas, con j de 1 a N.
iii) Itemset: conjunto o colección de ítems i_j y que contiene uno o más elementos.
iv) k-ítemset: ítemset formado por k elementos.
v) Hot encoding: binarización de una base de datos, indicando si el ítem correspondiente está o no presente en la transacción.
Por ejemplo:

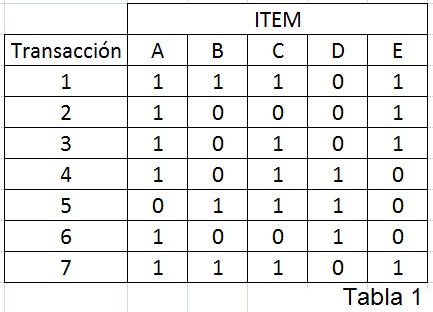
Luego, en la Tabla 1 puede leerse que en la transacción t₃ están presentes los ítems A, C y E (o contiene al 3-ítemset {A, C, E}).

Importante: Relación con Deep Learning
El Hot Encoding puede utiilizarse para expresar los datos de entrada y/o salida de una Red Neuronal Artificial cuando la característica relevante y digna de ser modelada se deriva de una lista de ítems, apariciones o presencia de variables booleanas (Ej: nublado o no, con viento o no, con frío o no, etc.).
Tipos de Hot Encoding: Multiple Hot Encoding (cuando se permiten varios 1s en cada vector) vs One Hot Encoding (cuando cada vector sólo puede tener un 1 y todos los demás valores iguales a cero). También existe el One Cold Encoding (cuando cada vector sólo puede tener un 0 y todos los demás valores iguales a uno).

vi)
Número de transacciones en las cuales el ítemset X está presente.
Por ejemplo, en la Tabla 1 el ítemset X = {A, C} está presente en cuatro transacciones (en t₁, t₃, t₄ y t₇).

Reglas de Asociación (RA)
Una RA corresponde a una afirmación condicional del siguiente tipo:

Donde X es un ítemset e Y es otro ítemset disjunto con X.
La RA se puede leer del siguiente modo:
Si el ítemset X está presente en una transacción, entonces el ítemset Y también estará presente en la transacción.
Por ejemplo:

De acuerdo con la Tabla 1, la RA falla en t₄.

Medición de la Validez de una RA
La validez de una RA se cuantifica por medio de tres métricas: S, C y L.
i) S: Support o Soporte de la RA :

Por ejemplo, utilizando los datos de la Tabla 1 y siendo la RA: , tendremos:
N = 7 (en total hay siete transacciones)

(corresponde a las transacciones t₁, t₃, t₇)
Luego
S = 3 / 7 = 0.43

ii) C: Confidence o Confianza de la RA :

Por ejemplo, utilizando los datos de la Tabla 1 y siendo la RA: , tendremos:

Luego
C = 3 / 4 = 0.75

iii) L: Lift o Levantamiento de la RA :
L = Prob(Y|X) / Prob(Y)
Por ejemplo, utilizando los datos de la Tabla 1 y siendo la RA: , tendremos:

Corresponde a las transacciones t₁, t₃, t₄ y t₇.
Considerando esas cuatro transacciones, el 1-ítemset {E} aparece tres veces.
Luego Prob(Y|X) = 3 / 4 = 0.75
Calculamos ahora la probabilidad de aparición del conjunto Y = {E]:
- Transacciones totales: N = 7
- Apariciones del ítemset {E}: 4
- Prob(Y) = Prob({E}) = 4 / 7 = 0.57
Finalmente:
L = Prob(Y|X) / Prob(Y) = 0.75 / 0.57 = 1.32
L > 1 => los ítemsets X e Y están positivamente correlacionados.

PARTE 2: Deep Learning
PASO 5 : Redes Neuronales Profundas
5.1 Qué es una Red Neuronal
El Conexionismo afirma que el comportamiento inteligente es capaz de emerger de redes o circuitos formados por simples unidades de procesamiento interconectadas (Donald Hebb, 1949). En el caso del cerebro humano, se afirma que la inteligencia emerge del cerebro, el que a su vez está formado por miles de millones de Redes Neuronales Biológicas (BNN), siendo la neurona la unidad mínima de procesamiento.
Para una Red Neuronal Artificial (ANN), tendremos el siguiente modelo:
- La actividad de una neurona es el valor arrojado por su "función de transferencia", cuyo argumento principal es la suma ponderada de la actividad de ciertas neuronas específicas
- Cualquier estado mental (pensamiento) es un vector n-dimensional que indica la actividad específica de cada una de las n neuronas presentes en el sistema
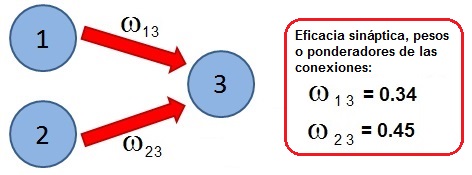
- La memoria o el aprendizaje queda grabado en los valores de los n x n ponderadores de las conexiones entre las neuronas (estos valores indican la "eficacia sináptica" de la conexión)
- Los valores óptimos de los n x n ponderadores se obtiene por medio de un Algoritmo de Aprendizaje o "Interferencia Adecuada".

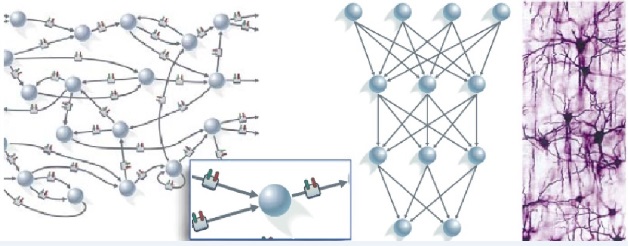
5.2 Alan Turing, fundador del Conexionismo En un innovador y sorprendente artículo sin precedentes y que permaneció inédito hasta 14 años después de su muerte, Alan Turing (1912-1954) describía en “Inteligent Machinery" una red de neuronas artificiales inicialmente conectadas al azar. En este tipo de cerebro denominado "Máquina Inorganizada tipo B" (abajo, izquierda), cada conexión pasa por un modificador ajustado por medio de cierta "Inteferencia Adecuada" (o Algoritmo de Aprendizaje), ya sea para dejar que los datos fluyan inalterados (fibra verde) o para destruir la información transmitida (fibra roja). Cambiando los estados de los modificadores por medio de la conmutación de sus modos, se puede adiestrar a la red y conseguir de este modo que pueda resolver cualquier problema específico, conviertiéndose así en un Sistema Experto. Observemos que cada neurona tiene dos entradas (recuadro inferior) y ejecuta una operación lógica sencilla, la negación de la conjunción (“NO-Y" o NAND): Si ambas entradas valen 1, la salida será 0. En caso contrario la salida valdrá 1. El manuscrito de Turing fue preparado para el Laboratorio Nacional de Física de Londres, pero no obtuvo la aprobación de la Institución. Sir Charles Darwin, nieto del naturalista evolutivo, dirigía el laboratorio como si fuera un colegio y desdeñó el trabajo de Turing, calificando las bases del Deep Learning como “ensayo de escolar”. En realidad, este artículo, de larga amplitud de miras, constituía el primer manifiesto en el campo de la Inteligencia Artificial y allí se encontraban diversas construcciones teóricas que posteriormente tuvieron que ser redescubiertas y reinventadas por otros científicos como Donald Hebb, Geoffrey Hinton, D.E. Rumelhart, J.L. McClelland y muchos otros. En la red de Turing las neuronas se interconectan libremente. En las redes modernas (abajo, centro) se suele restringir el flujo de información de una capa de neuronas a la siguiente. Los Conexionistas o especialistas en Redes Neuronales Artificales (ANN) imitan los circuitos neuronales del cerebro (abajo, derecha), obteniendo de este modo Inteligencia Artificial, la cual, no debería sorprender, también se sustenta en los trabajos de Alan Turing. De hecho, la denominación correcta de un computador es... Máquina de Turing.

5.3 Diadema Lectora de Pensamientos
Uno de los postulados del Conexionismo es: "Cualquier estado mental (pensamiento) es un vector n-dimensional que indica la actividad específica de cada una de las n neuronas presentes en el sistema ". Utilizando este postulado, la científica australiana Tan Le creó la empresa Emotiv Systems, cuyo producto estrella es una diadema lectora de pensamientos.

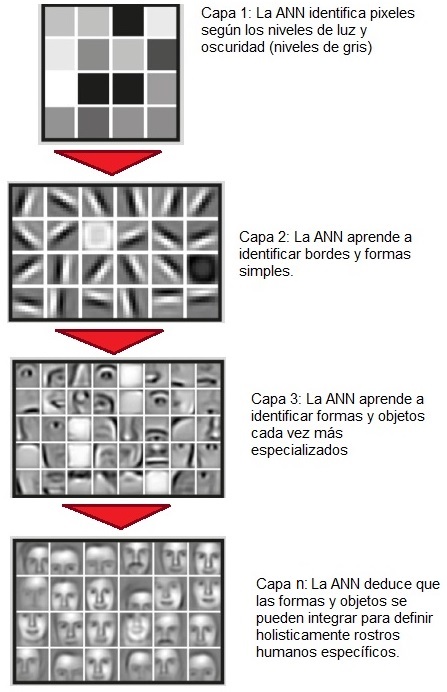
Ejemplo de Deep Learning: Reconocimiento Facial. Figura 2

5.4 ¿Qué hace que el Deep Learning sea "Deep"? El Deep Learning se identifica con un tipo especial de ANNs, donde la presencia de capas ocultas o intermedias permite que la Red Neuronal sea capaz de captar mayores niveles de abstracciones (Figura 2, a la izquierda). Matemáticamente esto se consigue por medio de transformaciones no lineales múltiples. En la práctica, la profundidad de una ANN está dada por la existencia de capas ocultas, de modo que cada capa n, propaga en reversa el error del aprendizaje de la capa n+1 por medio de lo que Alan Turing llamaba "Interferencia Adecuada". Esto comenzó a ser factible cuando Paul J. Werbos ideó el "Algoritmo de Retropropagación" en el año 1974, permitiendo de este modo la existencia de múltiples capas intermedias en una Red Neuronal. El Algoritmo ganó popularidad en 1986 cuando Rumhelhart, Hinton y Williams demostraron que el Algoritmo de Backpropagation logra enseñar a las unidades ocultas de procesamiento, de modo que éstas consiguen crear representaciones matemáticas "metafóricas" de los patrones presentes en las capas superiores. El término "Deep Learning" comenzó a ser utilizado en el año 2006 cuando Hinton, Osindero y Teh publicaron en Neural Computation el paper "A Fast Learning Algorithm for Deep Belief Nets", presentando Redes Neuronales cuyas capas exhiben jerarquías de abstracciones, consiguiendo de este modo un desempeño superior respecto de las ANNs clásicas. Conceptos Avanzados Deep Learning es una forma especial de implementar Machine Learning de modo que: - Se utiliza una secuencia o cascada de múltiples capas que poseen neuronas o unidades de procesamiento no lineal que permiten la extracción y transformación de las características clave de los patrones utilizados como input. - Cada capa utiliza como input el output de la capa inmediatamente anterior. - Puede ser implementado ya sea por medio de Aprendizaje Supervisado o No Supervisado - La ANN aprende múltiples niveles de representaciones que se corresponden con diferentes niveles de abstracción. Cada nivel de abstracción corresponde a una jerarquía de conceptos. - Para el aprendizaje se sirve de alguna forma de minimización de la función Error por medio de la Regla del Gradiente Descendente (Backpropagation).

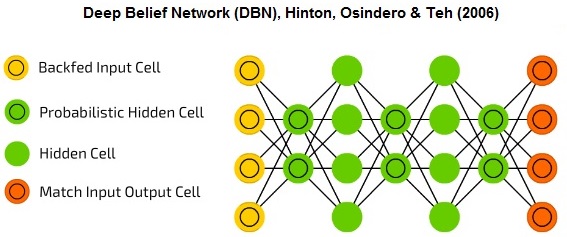Figura 3

---

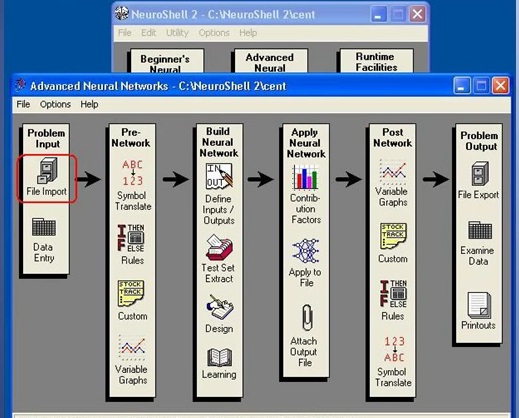
PASO 6 : Cómo crear una Red Neuronal Profunda (Aprendizaje Supervisado) - Ing. Jorge Reyes, NT2 Labs.

De acuerdo con el video, los pasos a seguir son: 1) Crear el archivo con los datos de entrenamiento 2) Crear el archivo con los datos de test 3) Importar ambos archivos 4) Configurar los campos o columnas. Es decir: - Especificar si el campo es input o output

- Especificar el valor mínimo de cada campo - Especificar el valor máximo de cada campo 5) Diseño de Red Neuronal - Paso 1: Escoger el tipo de ANN y configurar sus parámetros (como por ejemplo la cantidad de neuronas por capa). 6) Diseño de Red Neuronal - Paso 2:

Configurar la modalidad de entrenamiento y el criterio de detención del entrenamiento 7) Realizar el entrenamiento 8) Guardar la ANN final (guardar los pesos sinápticos) 9) Aplicar la ANN al archivo de set

PASO 7 : Mapas Autoorganizados de Kohonen (Aprendizaje No Supervisado)
7.1 Qué es un Kohonen SOM
Un Mapa Autoorganizado de Kohonen (Kohonen Self-Organizing Map) es una ANN que se entrena por medio de Aprendizaje No Supervisado (es decir, los vectores de entrada no incluyen la respuesta, solución esperada o "target output"). La ANN distribuye los vectores de entrada en grupos o clusters de acuerdo con los patrones que detecta durante la etapa de aprendizaje. En otras palabras, la ANN crea una representación discretizada o de menor dimensionalidad de los datos de entrada, de un modo semejante a como funciona la memoria asociativa en los seres humanos. Esta representación se denomina "Kohonen SOM" en honor de su creador, el Profesor finlandés Teuvo Kohonen quien la describió en la revista Biological Cybernetics en el año 1982.

7.2 Arquitectura de la Red La Red se puede visualizar como un arreglo 2D donde cada nodo está conectado a todas las neuronas de la capa de entrada. Si los vectores input son de dimensión n, entonces en la capa de entrada se tendrán n neuronas y la cantidad de pesos sinápticos de cada neurona del arreglo 2D con las neuronas de la capa de entrada será igual a n. Importante: Relación con Big Data Uno de los desafíos que enfrenta Big Data es el clustering de grandes volúmenes de datos (por ejemplo, identificar comunidades en una Red Social). Una ANN de Kohonen es capaz de clusterizar o agrupar vectores de un modo natural, es decir, sin tener que definir a priori un criterio de semejanza.

7.3 Algoritmo de Aprendizaje Competitivo (AAC)
Como se explicó inicialmente, los datos de entrada no incluyen un target output. En su lugar, para cada vector de entrada se selecciona una neurona especial denominada Best Matching Unit (BMU) y que es el centro del área de representación 2D del vector correspondiente. La sucesiva aplicación del AAC termina generando un mapa con zonas estables, de modo que cualquier nuevo vector que no haya sido visto durante la etapa de aprendizaje estimulará ciertas neuronas outputs que indicarán a qué zona del mapa pertenece este nuevo vector, análogo a como se activa la corteza cerebral humana cuando ésta recibe estímulos similares. Recordemos uno de los postulados fundamentales del Conexionismo: "Cualquier estado mental (pensamiento) es un vector n-dimensional que indica la actividad específica de cada una de las n neuronas presentes en el sistema ". Por lo tanto, estímulos similares generan actividades neuronales similares.

El AAC sigue los siguientes pasos:
1. Inicializar los pesos sinápticos de cada nodo.
2. Escoger aleatoriamente un vector input.
3. Determinar la neurona ganadora o BMU. La neurona ganadora es aquella cuyo vector de pesos sinápticos está más cerca del vector seleccionado en el paso 2.
4. Calcular el radio del vecindario de la BMU por medio de la siguiente igualdad:

5. Ajustar los pesos sinápticos de todas las neuronas dentro del vecindario de la BMU, de modo que se acerquen al vector input. Esto se realiza por medio de la siguiente igualdad:

6) Retornar al paso 2 hasta cumplir con el criterio de detención (n° total de iteraciones)

7.4 Ejemplo de Aplicación
Para cada ciudad de Chile Continental se creó un vector 7D con sus características sísmicas. A continuación una Red Neuronal de Kohonen clasificó cada vector dentro de uno de seis clusters, generando así una "Regionalización Sísmica de Chile". Como ilustración del resultado se puede mencionar que algunos de los vectores que cayeron dentro del cluster n°3 (sismicidad chilena "normal") fueron los asociados a las ciudades de Illapel, Vicuña y Antuco.
El SOM completo puede ser visto en el paper "A Chilean seismic regionalization through a Kohonen neural network" (año 2010).

 

PREGUNTAS

1) Big Data De acuerdo con la Tabla 1, la Confianza de la RA { A, E } => { B } es: a) 0 b) 75% c) 0.5

.

3) Redes Neuronales Artificiales (Perceptrón simple) Dada la siguiente ANN básica: Determine la actividad de la neurona eferente n° 3. Datos: Actividad de la neurona 1: 2; Actividad de la neurona 2: 1.75; Eficacia sináptica entre 1 y 3: 0.34; Eficacia sináptica entre 2 y 3: 0.45; Función de transferencia de 3: f(x) = 0.4 x + 1.9 Ayuda: El input de la neurona 3 será w13*(actividad 1) + w23*(actividad 2) El output de la neurona 3 será f(Input) a) 2.49 b) 1.47 c) 0.587

.

4) Kohonen SOM Según el Algoritmo de Aprendizaje Competitivo, los pesos sinápticos se ajustan de modo tal que a) El ajuste aumenta al aumentar la distancia a la BMU b) El ajuste se incrementa en magnitud al aumentar el n° de la iteración c) El ajuste disminuye con la distancia a la BMU

.