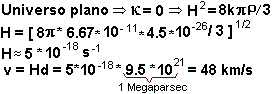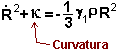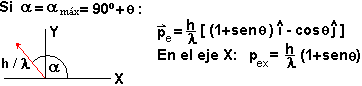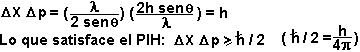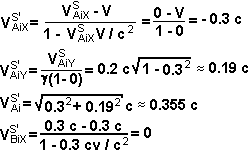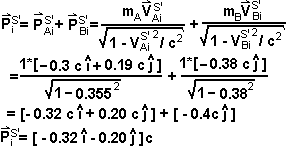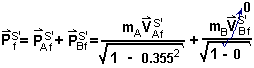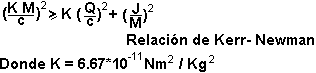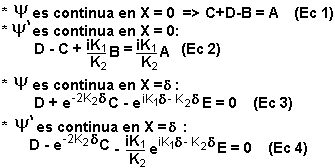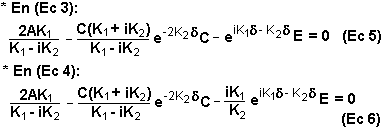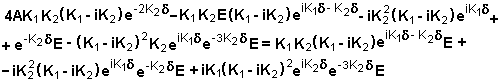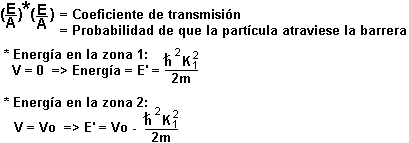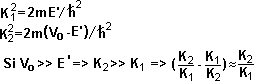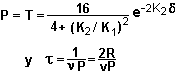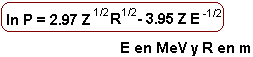CuánticaFÍSICA
MODERNA (Relatividad y Mecánica Cuántica)
"Mantente
doblegado
y permanecerás erguido.
Mantente vacío
y
permanecerás lleno.
Mantente usado
y permanecerás nuevo" Tao
Te King "Se
mueve
no se mueve.
Está lejos
pero está cerca.
Se
encuentra adentro
y está afuera" Isa
Upanishad |

Escudo
heráldico
de la familia Bohr | ¿Qué
está haciendo el electrón?
 "Si
preguntamos si la posición del electrón permanece constante, hemos
de responder que NO.
Si preguntamos
si la posición del electrón cambia en el tiempo, hemos de responder
que NO.
Si preguntamos si el electrón está en
reposo, hemos de responder que NO.
Si preguntamos si el electrón
está en movimiento, hemos de responder que NO." JR
Oppenheimer
|
"[El
Físico] al penetrar en los mundos más recónditos de la materia,
se ha percatado de la unidad esencial de todas las cosas y sucesos. Incluso ha
llegado más lejos y ha comprendido que él mismo y su consciencia
son parte integrante de esa unidad (...) Así, el Místico y el Físico
llegan a la misma conclusión (...) la armonía entre sus puntos
de vista confirma la antigua sabiduría hindú que dice que Brahman,
la Realidad Última Externa, es idéntica a Atman, la Realidad Interior"
(Fritjof Capra) |
|
CLAVES:
* Mecánica Cuántica
-
La Ecuación de Schrödinger corresponde a la versión cuántica
del Hamiltoniano Clásico (función energía)
- La solución
de la Ecuación de Schrödinger corresponde a una función que
contiene "comprimida" toda la información del sistema.
En esa función se encuentran las respuestas a cualquier pregunta posible.
Sólo hay que saber cómo preguntar. Esto se hace con el operador
cuántico correpondiente.
- La función de onda al cuadrado
corresponde a la probabilidad de que el sistema interactúe con el observador
(¿o "partícipe"?) por intermedio del canal de reacción
correspondiente.
* Relatividad General
La Ecuación de Campo
de Einstein (EFE) indica la inseparabilidad del par [EspacioTiempo] y [EnergíaMateria]
( = escenario y actores):

Donde:

Es
decir:
"La materia le dice al espacio como curvarse y el espacio le dice
a la materia como moverse"
O también: "Caminante no hay
camino, se hace camino al andar"
- Para un universo estático
(sin Big Bang) se requiere de una "gravedad repulsiva" para evitar el
colapso del universo por atracción gravitatoria. Esto se consigue agregando
una constante cosmológica " "
a la Ecuación de Gravedad de Einstein:
"
a la Ecuación de Gravedad de Einstein:
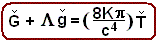
Posteriormente Hubble demostró que el universo
se encuentra en expansión (no es estático).
En palabras de Einstein:
"Postular una gravedad repulsiva fue el error más grande de mi vida"
....................................................................(...
Aunque algunos Físicos creen que no fue un error)
-
El tiempo y el espacio están fusionados, no son independientes. Las trayectorias
en el espacio de fases ya están dibujadas en el continuo (y estático)
EspacioTiempo. ejercicios propuestos de física
moderna

EJERCICIOS
RESUELTOS DE RELATIVIDAD ESPECIAL, RELATIVIDAD GENERAL Y MECANICA CUÁNTICA
1)
Relatividad Especial
La
masa de Clark Kent es de 90 Kg y su estatura es de 1.9 m. Sabiendo que Superman
vuela horizontalmente a 0.9c
a) Encuentre la estatura de Superman según
Luisa Lane (obviamente v(Luisa) --> 0 )
b) Encuentre la "masa relativista"
de Superman según Luisa Lane
c) Si para Superman transcurren 10 s,
¿Cuánto tiempo ha transcurrido para Luisa?
d) Compare (c) con
la situación de Clark Kent viajando horizontalmente en un avión
comercial a 800 Km/h
-----------------------------------------
a)
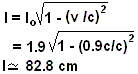
b)

NOTA:
La masa relativista sólo tiene sentido al vincularla con el momentum
c)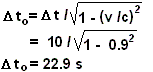
Así que los intervalos temporales de Superman
se dilatan <-----> Un segundo de Superman dura 2.3 s de Luisa
d)

Luego:

2)
MQ: Pozo de Potencial Impenetrable 1D
Sea una
partícula de masa m dentro de un pozo impenetrable 1D de longitud L:
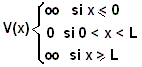
Encuentre
el valor esperado de la posición de la partícula.
-----------------------------
I)
La Ecuación de Schrödinger para 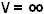 arroja la autofunción
arroja la autofunción 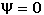
- La Ecuación de Schrödinger dentro del pozo (V = 0) es:

-
Solución:
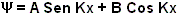
II)
Condiciones de Borde:

Por lo tanto:
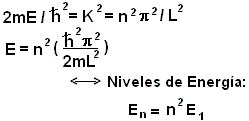
- Observemos que la mínima energía de la
partícula no puede ser cero, sino:
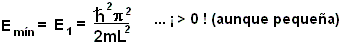
III)
Autofunción
- Por ahora:
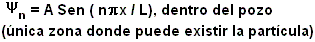
- ¿Cuánto vale A? ---> Condición de
normalización:
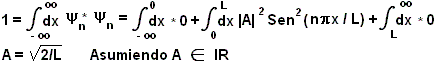
- Finalmente:
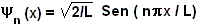
IV)
Valor esperado de la posición:

3)
Expansión Cosmológica

...
Sabiendo que la rapidez de alejamiento de las galaxias por
efecto de la expansión cosmológica es 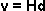 ,
encuentre la rapidez con la que se aleja una galaxia que se encuentra a 1 Megaparsec
de nosostros si el universo fuese plano
,
encuentre la rapidez con la que se aleja una galaxia que se encuentra a 1 Megaparsec
de nosostros si el universo fuese plano 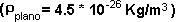
---------------------------------------------
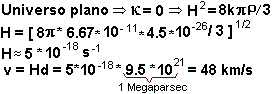
4)
Universos FRW
El radio de curvatura del universo
satisface la siguiente ecuación diferencial:
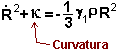
Analice
la evolución del universo si 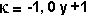
---------------------------------------
 corresponde a la densidad de materia en el universo, de modo que:
corresponde a la densidad de materia en el universo, de modo que:  .
.
Luego, la ecuación diferencial puede escribirse como:

* Si 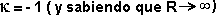 se obtiene:
se obtiene: 
Este es un universo "hiperbólico" 
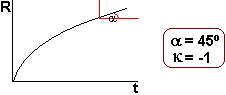
*
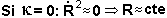
Este
es un universo "plano" (curvatura nula)

*
Este
es un universo "esférico" (curvatura positiva)

En
este último caso, la abundancia de materia en el universo es suficientemente
alta como para frenar el Big Bang e "intentar" compactarlo en un punto
por atracción gravitatoria.
5)
Principio de Incertidumbre de Heissenberg (PIH)
Se desea visualizar un electrón del modo "convencional" (con
luz). Para ello se dispara un fotón de longitud l,
de modo que el observador detecta la posición del electrón por medio
de la recepción del fotón reflejado en la "superficie"
del electrón. Demuestre que la incerteza en la posición del electrón
multiplicado por la incerteza en el momentum del electrón satisface el
PIH.
---------------------------------------------
El PIH es una característica
intrínseca del mundo microscópico. Las variables físicas
como la posición y el momentum están objetivamente indeterminados
y sus incertezas no provienen de problemas tecnológicos asociados a los
instrumentos de medición. La situación es al revés: según
el Principio de Correspondencia, cuando los números cuánticos (como
n, l y ml) son "grandes", el mundo cuántico se convierte
en clásico. Luego, podemos entender clásicamente el PIH mediante
"complicaciones" en el proceso de medición, teniendo presente
que esas complicaciones provienen de incertezas objetivas (p ej: el electrón
no está en una única posición, sino más bien está
en todas las posiciones posibles dentro de un rango  )
)
- Sea un electrón al que se le dispara un fotón. El fotón
se dispersará en un cono de luz caracterizado por un ángulo 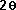 ,
de acuerdo con la siguiente figura:
,
de acuerdo con la siguiente figura:
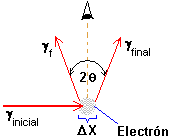
-
El observador recibirá un cono de luz (y no un rayo), el que cumplirá
con la ley de difracción:
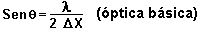
-
Luego, la posición del electrón se indetermina en: 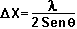
- Por otro lado, el fotón al golpear al electrón
provoca un cambio en el momentum del electrón:
->
Momentum inicial:

->
Momentum final del fotón:
El rayo de luz se convierte en un cono, de
modo que el momentum del fotón queda indeterminado dentro de un ángulo

-


- 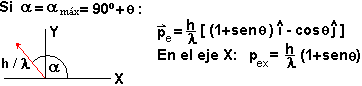
-
Luego, la incerteza en el momentum en el eje x del electrón es:
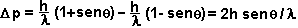
- Finalmente:
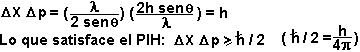
Es decir,
la incerteza experimental es mayor que la incerteza intrínseca del mundo
cuántico 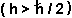
- Observemos que si queremos disminuir la incerteza en la posición del
fotón, tendremos que enviar fotones "cortos" (muy energéticos):

...
pero estropearemos la precisión del momentum:

(en
todo caso se sigue cumpliendo el PIH)
6)
Dinámica Relativista
Sea la siguiente
colisión 2D (mA = MB = 1 Kg) vista desde un sistema
S en reposo:
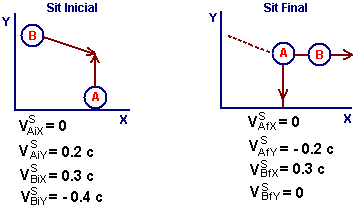
Demuestre
que el momentum se conserva cuando la colisión se observa desde un sistema
S' que se mueve con 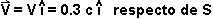
--------------------------------------------------------------
Según
Lorentz:
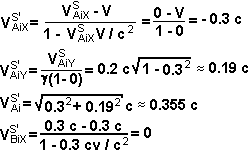


Luego
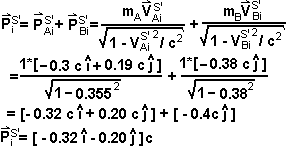
Por otro lado:
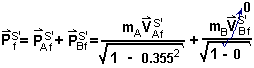

7)
Agujeros Negros
- El horizonte de Schwarzschild corresponde al radio bajo
el cual un cuerpo celeste se convierte en agujero negro
- El radio de Schwarzschild
es:

- En un agujero negro,
la rapidez de escape es mayor que c, cosa que es imposible de conseguir. De modo
que ni la luz puede escapar de la gravedad de un agujero negro (los rayos luminosos
"disparados" desde la superficie de un agujero negro "recaen"
hacia éste)
a) ¿Qué significa la relación de Kerr-Newman?
b) Encuentre la densidad que tendría que tener nuestro planeta para convertirse
en un agujero negro (MT = 6*1024 Kg)
c) Encuentre la
energía máxima que se puede extraer desde un agujero negro, dados:
- Teorema del área: la superficie del horizonte de eventos de un agujero
negro nunca puede disminuir en el tiempo
- La superficie del horizonte de
un agujero negro es:
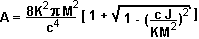
-
La rotación máxima (momentum angular) que puede conseguir un agujero
negro es: 
- La superficie máxima del horizonte de eventos es: 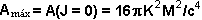
--------------------------------------------------------------
a) Los agujeros
negros satisfacen la relación:
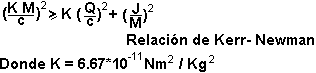

...
La relación contiene todas las soluciones triparamétricas (M, Q
y J) conocidas que describen a los agujeros negros. Utilizando esta desigualdad
se puede llegar a concluir que el desplome gravitatorio total de un cuerpo celeste
siempre produce un agujero negro del tipo Kerr-Newman.
- Si J = 0 se obtiene
un agujero negro de Schwarzschild
- Si J = KM2/C, se obtiene un
agujero negro de Kerr (en rotación máxima)
b)
Para nuestro planeta:

c)
Si partimos con un agujero negro cuya superficie sea mínima <--->
en rotación máxima:
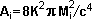
Y luego se extrae energía 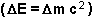 ,
la nueva superficie siempre será menor o igual que la máxima:
,
la nueva superficie siempre será menor o igual que la máxima:
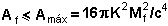
Según el Teorema del
área: 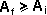
Es decir:
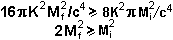
Luego, en el
caso extremo: 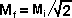
De modo que

Por lo tanto,
en un agujero negro se puede extraer hasta el 29.3% de la energía original
(v/s fusión de hidrógeno en helio: apenas ~ 1%)
8)
Desintegración alfa (Gamow, Gurney y Condon, 1928)
...
Encuentre la probabilidad de desintegración por emisión alfa, asumiendo
que la partícula alfa siempre existe y que se encuentra atrapada entre
dos barreras de potencial de altura Vo:
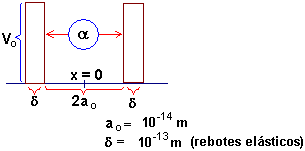
--------------------------------------------------------------
i) Probabilidad de desintegración y vida media.
Según Gamow:
- La barrera de potencial se ubica entre x = R y x = r1, siendo
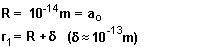
- Se asume que la partícula
alfa siempre existe dentro de la barrera de potencial
- La partícula
alfa choca repetidamente contra la barrera
- Entre choque y choque la distancia
recorrida es 2R
- Luego, la frecuencia de los choques es 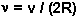
- Sea P la probabilidad de traspasar la barrera por efecto túnel. La desintegración
alfa ocurre cuando la partícula alfa consigue traspasar la barrera
- La probabilidad de desintegración por unidad de tiempo será 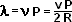 .. y la vida "promedio" (o "esperada")
será
.. y la vida "promedio" (o "esperada")
será 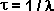
ii)
Barreras de potencial
- Las barreras pueden ser modeladas del siguiente modo:
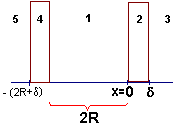
Observemos que la probabilidad
de traspasar la barrera de la derecha (2) es igual a la probabilidad de traspasar
la barrera de la izquierda (4)... => estudiaremos
la barrera de la derecha.
iii) Funciones de onda
- En la zona 1, la partícula se mueve hacia adelante y hacia atrás:
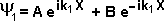
- En la zona 2 se encuentra
la barrera de potencial:

- Si la partícula se encuentra en la zona 3 es porque fue expulsada del
núcleo ... => se mueve obligatoriamente
hacia la derecha

iv)
Condiciones de borde:
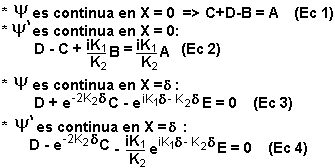
v)
El coeficiente de transmisión de la barrera es:

- Reemplazando D en (Ec 3) y (Ec 4):
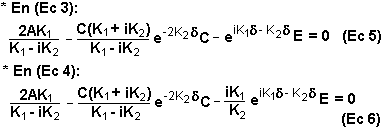
- Despejando C desde la Ec 5:

- Igualando

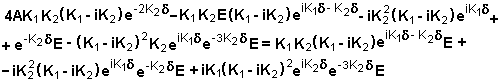

Observemos que:
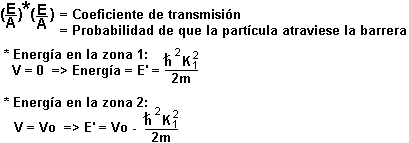
vii) Aproximaciones
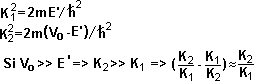
Sea el espesor de la barrera lo suficientemente grande como para atenuar
el haz, de modo que 
Luego:

La probabilidad de transmisión
será:
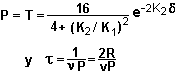
Observemos
que:


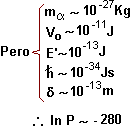
viii)
Gamow observó que la expresión

Finalmente:
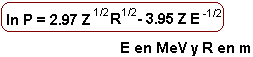
Tema
Relacionado: Viviendo en una Matrix
Registro de Propiedad
Intelectual Nº 154.044 © GeoEnterprises - Todos los derechos reservados
Se permite la reproducción parcial con tal que se cite la fuente: "TGT-
www.fum.cl"
Oscilador Armónico
Simple Ecuación de Schrödinger Principio de Incertidumbre de Heissenberg
Niels Bohr Principio de Exclusión de Pauli Enlace covalente Espectro moléculas
Teoría de la Relatividad Especial y General Agujero Negro Big Bang Big
Crunch Transformadas de Lorentz Albert Einstein Efecto Fotoeléctrico Dispersión
Compton fotón De Broglie Experimento de las rendijas