Mecánica
HOME
Registro de Propiedad
Intelectual nº 154.044

Mecánica - Reduccionismo - Atomismo - Antisinergia
Para entender el todo basta con comprender como funcionan las partes y a continuación éstas deben ser reensambladas para volver a tener el sistema original.

La clave de la Mecánica reside en el concepto de "partícula" y en la función llamada "Hamiltoniano" (o "Lagrangiano"). El concepto de "partícula" consiste en una abstracción de la realidad física, donde sólo se incluyen las propiedades que consideramos relevantes. Por otro lado, el Hamiltoniano corresponde a la función energía. Si somos capaces de escribir la energía de un sistema, entonces seremos capaces de resolver cualquier problema - habido y por haber - que pueda plantearse sobre el sistema en cuestión. En otras palabras, la función energía contiene todas las respuestas a las preguntas que se pueda plantear sobre el sistema.
Cabe señalar que la Mecánica es una "Teoría Realista Local", lo que significa que se realizan tres aproximaciones:
- El término "Teoría" indica que no se duda de la inducción (o del empirismo) como el método por antonomasia para llegar a la verdad.
- El término "Realista" quiere decir que se asume que existe un mundo externo e independiente del observador.
- El término "Local" significa que como máximo las interacciones viajan a la rapidez de la luz (3x108m/s)
Hay otras aproximaciones (como la que dice que las proposiciones ó son verdaderas ó son falsas), pero aquí no hablaremos de ellas.





EJERCICIOS TÍPICOS DE MECÁNICA

1) Vectores
Un pequeño telescopio se encuentra en (2, 2.3, 3) Km y se desea visualizar la cima de un cerro que se encuentra en (5, 7, 3.3) Km. Encuentre los ángulos respecto de los tres ejes en los que debe estar orientado el telescopio para poder observar la cima del cerro.
R:
2) Movimiento Uniformemente Acelerado
Un jugador de béisbol X1 batea la bola a 1 m de la superficie y le imprime una rapidez de 14 m/s con un ángulo de 30° respecto de la horizontal. En ese mismo instante, un segundo jugador X2 (a 25 m de X1) comienza a correr con rapidez constante y alcanza la bola a 2.4 m sobre la superficie. Encuentre la rapidez mínima de X2
R: v = 8.9 m/s
3) Las Leyes de Newton
Un bloque de 5 Kg sube por un plano inclinado a 30° , con una rapidez inicial de 40 m/s. El bloque alcanza una altura máxima h y luego retorna a la posición inicial. Enuentre: (a) La altura h, (b) El tiempo ocupado en retornar
R: (a) 53.3 m , (b) 2.21 s en subir y 5.6 s en bajar
4) Trabajo y Energía
 a) ¿Cuál es la energía necesaria que debe imprimir la mano de un karateka para romper un madero de volumen V y módulo de Young Y, sabiendo que el madero soporta una presión máxima igual a P?
b) En 1840 el Médico y Naturalista alemán J Mayer se embarcó en un buque holándes hacia la isla de Java. Mayer observó que el color de la sangre venosa de los marineros era más roja en Europa que en la isla de Java. ¿Conclusión?
c) Encuentre la altura a la que llega un objeto de 3 Kg de masa de acuerdo con la siguiente figura:

R: a)
b) En las latitudes frías (Europa) para mantener constante la temperatura del cuerpo es necesaria una mayor oxidación de los alimentos consumidos (Equivalencia entre calor y trabajo)
c)

5) Hamiltoniano y Lagrangiano
 a) Encuentre el Hamiltoniano para un oscilador armónico simple
b) Encuentre el Hamiltoniano del siguiente sistema:

R:

6) Sistema de Partículas
 a) Un misil es lanzado con v0= (0, 500, 500) m/s, explotando en el aire en dos esquirlas iguales. Los soldados encuentran una esquirla en (5, 40, 0) Km. ¿A qué punto hay que enviar a l otro batallón para que encuentre la otra esquirla?
b) En la siguiente reacción química: Na + Cl --> NaCl, encuentre el porcentaje de energía que se libera como calor, sabiendo que:
- m(Na)= 23 uma, m(Cl)= 35.5 uma
- v(Na)= +1500 m/s, v(Cl)= -1000 m/s
- La masa se conserva
R: (a) Al punto (-5, 60, 0) Km , (b) 39.3%
7) Dinámica de Rotación
 a) Hace 65 millones de años un cometa colisionó con la Tierra y aplicó un torque de 1031 J que actuó durante 85 s, lo que provocó una rotación más rápida de nuestro planeta. Sabiendo que I(Tierra) = 1.25x1038 Kgm2, encuentre la duración del día terrestre antes de la colisión.
b) Un electrón en el átomo de Hidrógeno se encuentra en la segunda capa. El electrón se trraslada en sentido horario en el plano XY y el spin es igual a (0,0, h/(4*pi)). Encuentre el momentum angular total.
Datos:
- r = 2.12x10-10 m
- v = 1.11x106 m/s
- m = 9x10-31 Kg
- = 1.055x10-34 Js

R: a) 26.5 horas
b)
8) Movimiento Armónico Simple
 Un cilindro de caucho de 50 cm de largo se estira 20 cm respecto del punto de equilibrio después de colocarle una masa de 0.016 Kg. Encuentre: (a) La energía mecánica almacenada por el sistema (Y = 50 N/m2, diámetro del cilindro: 10 cm), (b) El periodo de la oscilación
R: (a) 0.0158 J, (b) 0.89 s
9) Ondas
 a) Sea una ola propagándose hacia la derecha Z1= 2Sen(- t + y) metros y otra ola propagándose hacia la izquierda Z2= 2Sen(y + t). Encuentre la ola resultante.
b) La Dra Sattler de Jurassic Park desea encontrar la profundidad del basamento rocoso mediante la inducción de una tronadura. Sabiendo que:
- Hay dos capas: suelo y roca
- V(sonido en el suelo)= 2000 m/s, v(sonido en la roca)= 3500 m/s
- t(onda directa) = 1 s, t(onda reflejada) = 2 s
Encuentre:
b.1) La profundidad del basamento rocoso
b.2) El ángulo necesario para obtener "Reflexión Interna Total"
c) Una órbita "permitida" en el átomo de hidrógeno se puede interpretar como aquel perímetro donde la onda de electrones se "auto-interfiere" constructivamente. Encuentre:
 c.a) Los radios permitidos
c.b) Los valores posibles para la energía cinética
R: a) Z= 4 Sen y Cos t (Onda estacionaria)
b.1) 1.73 Km
b.2) 34.9°
c):
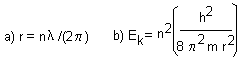
10) Fluídos
 a) Un recipiente de altura h y de gran sección transversal ("boca ancha") se encuentra albergando agua y tiene un orificio en la mitad de su altura. Deduzca la rapidez con la que sale expulsada el agua por el orificio
b) Se tiene un acuífero en reposo de modo que en el punto X1 comienza a una profundidad h1, mientras que en el punto X2 comienza a una profundidad h2 (h1 > h2). Encuentre la diferencia de presión entre X1 y X2.
R: (a) (gh) 1/2 (b) P1- P2 = Rho* g*(h1- h2)

EJERCICIOS RESUELTOS

1) Un cuerpo de masa m1= 10 g con una rapidez de 2 m/s en el plano superior, impacta elásticamente a un cuerpo de masa m2 = 20 g que se encuentra detenido en el plano inferior. Encuentre:
a) La compresión máxima experimentada por el resorte (k = 2.5 N/m)
b) El tiempo durante el cual m2 permanece en contacto con el resorte
c) La altura que alcanza m1 sobre el plano inclinado después de la colisión
 ---------------

a) Para m1:

Choque elástico, luego: ( i )
( ii )

Luego, la Energía de m2 es:

b) m2 permanece en contacto con el resorte durante un semiperiodo, es decir:

c)

2) Odontología
 Se tiene el cráneo fijo y la mandíbula móvil respecto del punto A. Mientras se mastica, una muela cilíndrica ( l = 2 cm, r = 0.5 cm, E = 500 000 N/m2) recibe la siguiente fuerza:

Encuentre:
a) La deformación vertical experimentada por la muela
b) El torque ejercido por respecto de A
c) El sentido de la rotación en el eje X
d) Si la inserción de los músculos masticatorios está en , encuentre la fuerza mínima que deben ejercer para mantener la mandíbula inmóvil (masa de la mandíbula despreciable)
----------------------------
a)
b)
c) la rotación en el eje X es antihoraria (la mandíbula tiende a abrirse)
d)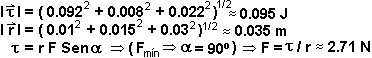

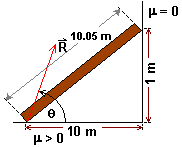
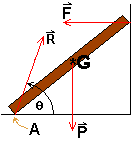
3) Estática
Sabiendo que la siguiente escalera (m = 15 Kg) no desliza, encuentre el ángulo entre la reacción "R" y el suelo.
-----------------------------------------------------------------
* Fuerza de reacción:

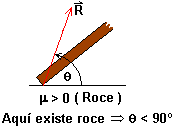
* Reacción de la pared: porque aquí no existe roce

DIAGRAMA DE CUERPO LIBRE


4) Dinámica
Dado un cuerpo y un plano inclinado, encuentre la fuerza mínima necesaria para que el cuerpo baje con velocidad constante.

------------------------------------------------------



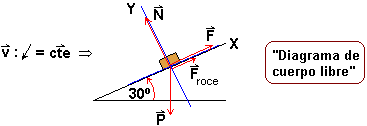
(Sugerencia: encuentre si el cuerpo sube con cuando el ángulo entre y el eje X es de 30º.
R: )

5) Gravitación Universal (cálculos clásicos)
a) Encuentre g en función de r
b) Encuentre la rapidez mínima que debe tener un proyectil para escapar de la gravedad terrestre
c) Encuentre el radio que debe tener la Tierra para que la "velocidad de escape" sea igual a c = 3*108
---------------------------------------------------------------

b) El proyectil escapa


Equivale al radio mínimo necesario para que la Tierra se convierta en un "agujero negro"

6) Rotaciones
Dado el siguiente diagrama:

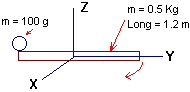
La pequeña esfera se encuentra inicialmente fija al extremo de la barra y el sistema está girando a 10 rad/s.
Encuentre
a) del sistema
Si la esfera pierde contacto con la barra, (b) ¿Con qué rapidez sale disparada?
c) ¿Cuál debe ser la magnitud mínima del torque que consigue detener la barra después de 5 revoluciones?
---------------------------------------------------------------------



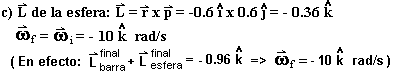
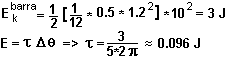
7) Fluídos
Dado el siguiente diagrama:

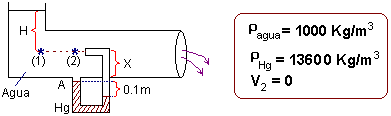
Encuentre:

-----------------------------------------------------------------
a) Para el manómetro:



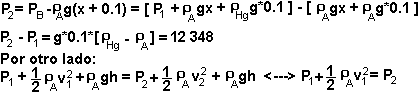
ONDAS
8) Prospección Sísmica
Se provoca una tronadura en E con el objetivo de delimitar un acuífero:

Encuentre el ángulo de incidencia, el ángulo de refracción y la profundidad (vertical) a la que se encuentra el acuífero respecto de R.
--------------------------------------------------------------------
* Angulo de incidencia


* Angulo de refracción

* Profundidad respecto de R:

9) De Broglie
Encuentre los radios permitidos en el átomo de hidrógeno en función de la rapidez del electrón, sabiendo que (De Broglie)
--------------------------------------------------------
Para que el electrón esté en resonancia, debe "autoprovocarse" interferencia constructiva, es decir:
Perímetro = n l

Registro de Propiedad Intelectual Nº 148.917 © GeoEnterprises - Todos los derechos reservados
Se permite la reproducción parcial con tal que se cite la fuente: "TGT- www.fum.cl"

Cinemática Dinámica Estática Las Leyes de Newton Lanzamiento de proyectiles caída libre ondas óptica gravedad gravitación universal momentum momento torque par fluídos plano inclinada fuerzas masa inercial algebra vectorial