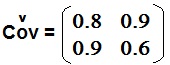PASO 1: Bienvenida - Prof. Heidi Bilbao, MT Trading

Importante
En el curso completo de XLStat y @Risk, ya sea en su versión web (USD 210) o en la versión presencial de 24 horas (USD 370), se tratan muchísimos más temas y con el máximo detalle posible. El siguiente es el temario del curso completo:
Parte 1: XLStat
- Descripción de XLSTAT
- Análisis de Componentes Principales
- Muestreo de datos, muestreo de distribuciones y codificación por rangos.
- Estadísticos descriptivos e Histogramas.
- Pruebas de Correlación/Covarianza
- Prueba T y prueba Z
- Prueba de comparación de varianzas.
- Regresión lineal simple y múltiple
Parte 2: @Risk
- Descripción del Programa
- Qué es una simulación Monte Carlo
- Qué es un muestreo Latino Hipercúbico
- Funciones de distribución de Probabilidad
- Interpretación del Informe por medio de un ejemplo financiero.
- Aplicación n°1: Aplicación sobre explotación de Recursos Naturales.
- Aplicación n°2: Six Sigma. |
| Sitio web de XLStat / Addinsoft: www.xlstat.com/es/empresa |
Sitio web de @Risk / Palisade: www.palisade-lta.com/risk |
Otros talleres gratuitos de MT Trading
Inteligencia Artificial, Deep Learning y Big Data | Gestión de Proyectos por medio del PMBOK
|
PARTE 1: XLStat
PASO 2: Qué es XLStat
El complemento estadístico XLStat para Excel, ha sido desarrollado por la empresa Addinsoft y se instala como un complemento o nueva barra en la cinta de opciones de MS Excel, tal como puede verse en la siguiente figura:
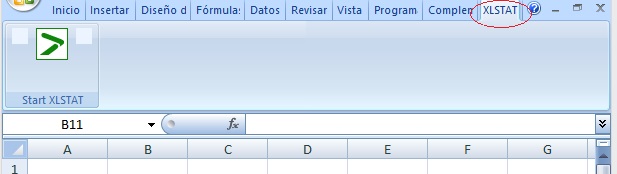
El complemento permite realizar análisis estadístico e incluye más de 200 herramientas dentro del entorno o interfaz de Excel, razón por la cual el usuario parte familiarizado con la modalidad de trabajo.
|
Addinsoft considera que las siguientes herramientas son las más utilizadas, razón por la cual se incluyen en "XLStat - Free Edition":
1) Muestreo de datos.
2) Muestreo de distribuciones.
3) Codificación por rangos.
4) Estadísticos descriptivos
5) Histogramas.
6) Pruebas de Correlación/Covarianza
7)
Prueba T y prueba Z
8) Pruebas de comparación de varianzas.
9) Pruebas no paramétricas para 2 muestras (prueba de Wilcoxon, prueba de signos, prueba de Mann-Whitney)
10)
Regresión lineal simple y múltiple
11) ANOVA de una y dos vías para datos balanceados y no balanceados
12) Suavizado de series temporales incluyendo medias móviles y exponenciales.
13) Transformadas de Fourier. |
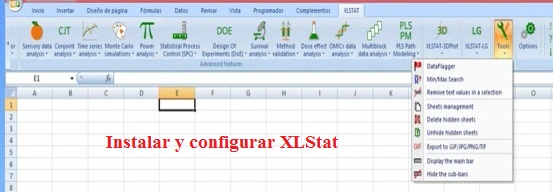
PASO 3: Instalando y configurando XLStat - Ing. Jorge Reyes, NT2 Labs.
* Descargue el instalador de XLStat (versión de prueba gratuita habilitada por 30 días) desde aquí: www.xlstat.com/es/descargar
* A continuación realice el procedimiento explicado en el siguiente video:
Importante
1) XLStat se instala como un complemento de Excel en la cinta de Opciones.
2) El complemento instalado se denomina "XLSTAT Starter" y se encuentra en C:/Program Files/Addinsoft/XLSTAT/XLSTATRIB.xlam |
3) La extensión xlam corresponde a "MS Excel Open XML macro enabled add-in file", o archivo de complemento (add-in) de MS Excel habilitado para macros en Visual Basic for Applications.
4) Para permitir la ejecución de las macros de XLStat, se debe "Confiar en el acceso al modelo de objetos de proyectos de VBA". |
PASO 4 : Conociendo XLSTAT.
La cinta de opciones XLSTAT posee los siguientes grupos:

(1) Grupo Reciente; (2) Grupo Descubrir, explicar y predecir; (3) Grupo Testear una hipótesis; (4) Grupo Herramientas avanzadas; (5) Otros Grupos.
En este Taller básico, utilizaremos la opción "Análisis de Componentes Principales (ACP)", que se encuentra dentro de "Análisis de Datos" en el Grupo "Descubrir, Explorar y Predecir".
PASO 5 : Principal Component Analysis.
En qué consiste el Análisis de Componentes Principales (ACP) - Ing. Jorge Reyes, NT2 Labs.

Importante
1) El ACP se emplea en el Análisis Exploratorio de los Datos con el objetivo de caracterizar la dispersión de éstos. Específicamente se encuentra en primer lugar la dirección en la cual la dispersión es máxima, de modo que ese eje es el que contiene la mayor información del dataset (a mayor variabilidad, mayor será la información y la entropía de Shannon).
Por ejemplo, para cierto dataset de pacientes de un hospital caracterizados por la Edad (eje X) y la Presión Arterial (eje Y) se puede descubrir que los puntos 2D tienden a agruparse en torno de una línea orientada a 25° respecto del eje X, es decir, en la dirección (Cos(25°), Sen(25°)) = (0.906, 0.423). Por lo tanto, la variable importante no es ni la Edad por sí sola, ni la Presión Arterial por sí sola, si no la siguiente nueva variable: 0.906*Edad + 0.423*Presión Arterial.
2) El ACP permite obtener vectores propios o direcciones perpendiculares entre sí jerarquizadas según el aporte a la variabilidad de los datos. Los vectores propios se ordenan de acuerdo con sus valores propios respectivos (de mayor a menor), de modo que el primer eje o componente principal será el que explica el mayor porcentaje de variabilidad de los datos. Si los valores propios se expresan porcentualmente (dividiendo el valor propio respectivo por la suma de todos los valores propios) el valor obtenido corresponderá a la fracción de información que se proyecta o contiene el vector propio o la dirección respectiva.
3) Según John W. Tukey. el Análisis Exploratorio de los Datos (EDA) pemite caracterizar estadísticamente un dataset e incluye dos pasos:
* Medición y descripción por medio de promedios y dispersiones (aquí se incluye ACP)
* Comparaciones e inferencias (Histogramas, Tablas de Contingencia, etc.)
4) El ACP ordena descendentemente las direcciones de acuerdo con el grado con el cual consiguen explicar la variabilidad de los datos. La variabilidad puede ser medida de tres maneras:
* Manera clásica: Variabilidad según la Matriz de Correlaciones (de Pearson)
* Variabilidad según la Matriz de Covarianzas: Se asigna mayor peso a las variables con varianzas más altas.
* Variablidad según la Correlación de Spearman: Es adecuado cuando las variables presentan distribuciones diferentes de modo que se minimiza el aporte a los cálculos de los valores atípicos (la correlación de Spearman es menos sensible que la correlación de Pearson cuando existen valores atípicos disparados en los extremos de las distribuciones).
5) El ACP asume como verdaderos los siguientes supuestos:
a) Linealidad: se asume que el dataset es generado por una combinación lineal de cierta base vectorial inicialmente desconocida.
b) Dispersiones gaussianas: se asume que la dispersión en torno de cada eje principal queda bien representada con distribuciones normales. |
PASO 6 : Cómo realizar ACP en XLSTAT
6.1. ACP - Procedimiento a seguir / Ing. Jorge Reyes, NT2 Labs
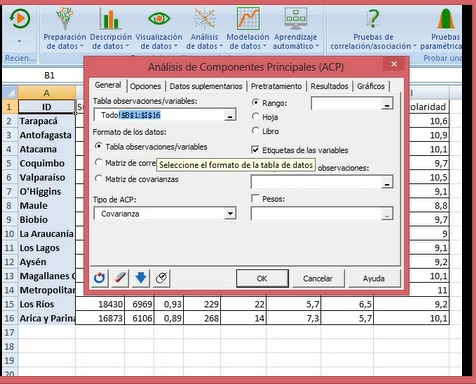
Importante: Excel avisará que el archivo tiene macros, razón por la cual éste tiene que ser guardado con el siguiente formato:"Libro de Excel habilitado para macros".
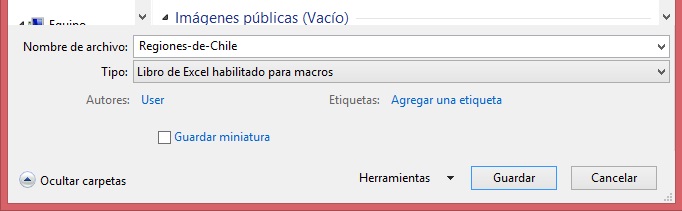
6.2. ACP - Interpretación del Informe de Análisis de Componentes Principales.
Dataset utilizado:
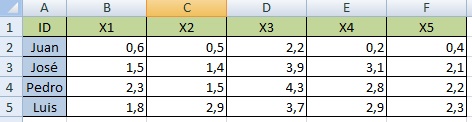
Ejes utilizados para graficar: F1 y F2

El informe de ACP que se obtiene es el siguiente: |
|
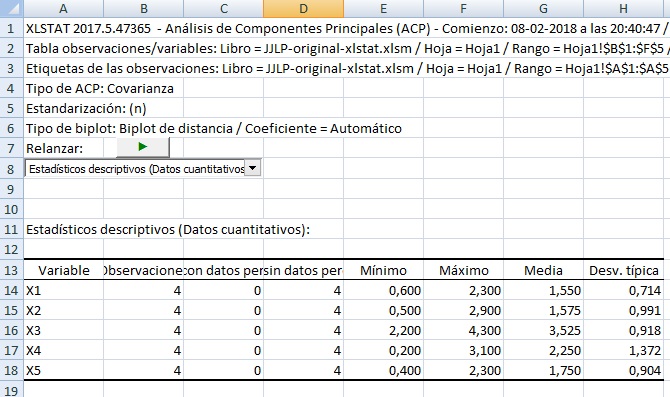
Las primeras filas son las filas de encabezado, incluyendo el tipo de matriz utilizada (covarianzas). La lista desplegable es un índice que pemite saltar al marcador seleccionado.
En la fila 11 comienzan los estadísiticos descriptivos de cada eje original (desde x1 a x5), indicándose en la tabla que comienza en A13 lo siguiente: número de observaciones, datos pérdidos, datos no pérdidos, valor mínimo, valor máximo, media y desviación típica.
|
|
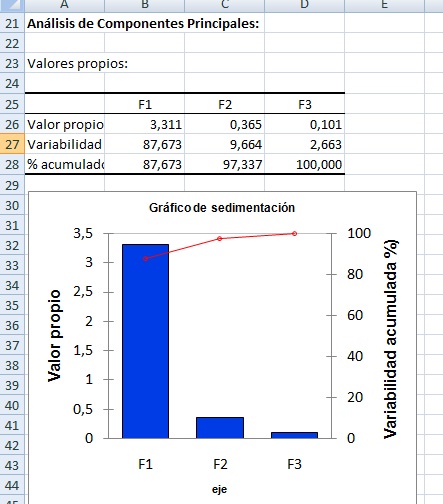
En A25 comienza la tabla de los valores propios de cada eje principal.
* El autovalor del eje F1 es 3.311 (B26), explicando el 87.673% de la variabilidad (B27). Este eje por sí solo es una buena proyección 1D de la tabla multidimensional inicial dado que proyecta el 87.673% de la información contenida en el dataset.
* El autovalor del eje F2 es 0.365 (C26), explicando el 9.664% de la variabilidad (C27). El porcentaje de variabilidad proyectado en F1 más F2 es B7 más C27, es decir 97.337% (C28).
* El autovalor del eje F3 es 0.101 (D26), explicando el 2.663% de la variabilidad (D27). El porcentaje de variabilidad proyectado en F1 más F2 más F3 es B7 más C27 más D27, es decir 100% (D28).
En el gráfico de sedimentación se observa:
* El histograma de colummnas azules se asocia al eje vertical de la izquierda
y corresponde a los autovalores.
* La curva roja se asocia al eje vertical de la derecha y corresponde al porcentaje de variabilidad acumulado. |
|
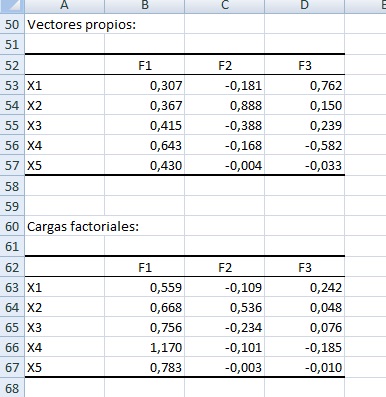
* Los vectores propios (o factores) se leen en la tabla que comienza en A52 y se leen verticalmente hacia abajo. Por ejemplo, el primer eje principal se lee con los datos del rango B53 a B57 y corresponde a:
0.307 en la dirección del eje X1
0.367 en la dirección del eje X2
0.415 en la dirección del eje X3
0.643 en la dirección del eje X4
0.430 en la dirección del eje X5
NOTA: en esta tabla los vectores propios están normalizados a uno, pero una ponderación también es válida. Por ejemplo, (1, 3) y (0.32, 0.95) son vectores que apuntan en la misma dirección.
La matriz de cargas factoriales "A" se presenta en B63:D67 y es la pendiente multidimensional que relaciona el vector columna de los ejes iniciales (X) con el vector columna de los ejes principales (F) por medio de la siguiente igualdad:
X = A F + u
Siendo u el intercepto.
|
|
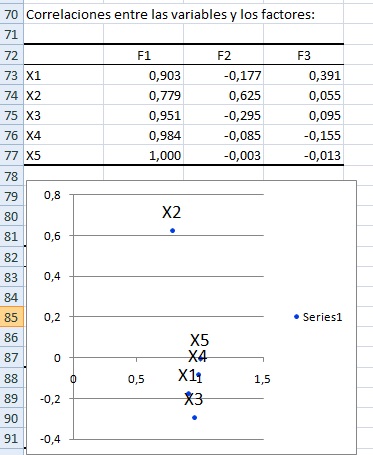
La matriz de correlaciones se presenta en B73:D77 y muestra la corelación entre cada variable inicial (X1 a X5) y los ejes principales.
Por ejemplo:
- Correlación entre X2 y F1: 0.779
- Correlación entre X2 y F2: 0.625
Es decir, en el plano F1, F2 la correlación de X2 se resume en el siguiente par ordenado: (0.779, 0.625). Puede verificarse que ésto es así revisando el gráfico que comienza en A79.
Hemos hablado aquí de los ejes F1 y F2 porque esos fueron los ejes seleccionados inicialmente:

|
|
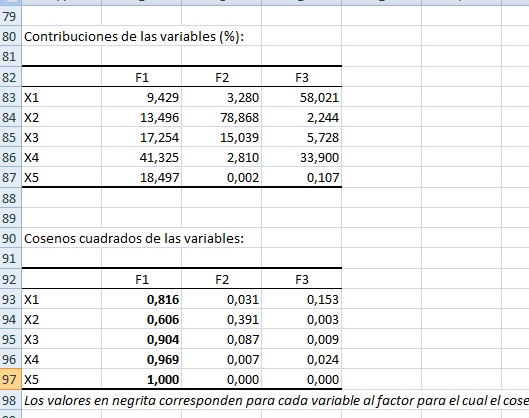
En B83:D87 se presentan los aportes porcentuales de cada variable a cada eje principal y se calculan como la componente al cuadrado del vector normalizado. Por ejemplo B83 vale 0.9429 (o 9.429%) porque ese es el valor de B53 al cuadrado (aproximadamente).
En A92 comienza la tabla de los cosenos al cuadrado. Dado que B93 vale 0.816, entonces el ángulo entre X1 y F1 vale 25.401°, ya que
[ Cos(25.401°) ]2 = 0.816
|
|
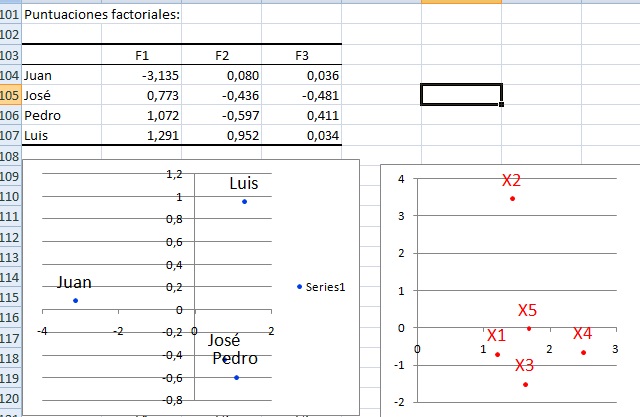
En B104:D107 aparecen los registros (desde Juan a Luis) escritos en función de los ejes principales.
Por ejemplo, Juan es igual a -3-135 en la dirección F1, más 0.080 en la dirección F2, más 0.036 en la dirección F3.
El gráfico con puntos azules de la izquierda muestra los cuatro registros en el sistema de cordenadas F1 F2.
El gráfico con puntos rojos a la derecha muestra los ejes originales (desde X1 a X5) proyectados en los ejes principales F1 F2. |
|
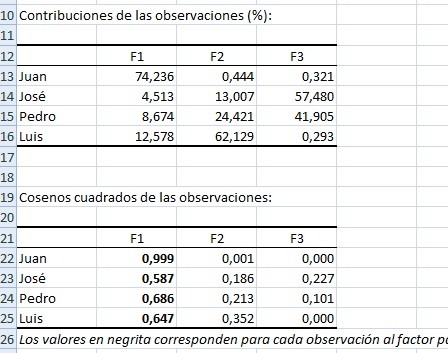
En la tabla que comienza en A112 se observan las contribuciones porcentuales de cada registro a cada eje, de modo que la suma por columna (o eje principal) es 100%.
En la tabla que comienza en A121 se observan los cosenos al cuadrado de las observaciones en función de los ejes principales. Por ejemplo, si se normaliza "Pedro" a uno, el versor será (0.83, -0.46, 0.32) y corresponde a los cosenos directores del versor de Pedro en función de los ejes principales. Luego, si elevamos la primera componente a dos, se obtendrá B124 (aproximadamente). |
PARTE 2: @Risk
|
PASO 7:
Qué es @Risk / Introducción a Funciones de Densidad de Probabilidad.
7.1 Qué es @Risk
@Risk es un complemento de Excel desarrollado por Palisade Corporation y que permite modelar escenarios donde sólo se conoce el comportamiento probabilístico de ciertas variables, de modo que el resultado final puede variar según los valores de los datos de entrada seleccionados en la iteración respectiva. Los datos de entrada pueden seguir diversos tipos de distribuciones como: Beta, Exponencial, Normal, Gamma, etc. Lamentablemente los computadores sólo saben simular distribuciones uniformes pseudoaleatorias, de modo que ¿Cómo construímos otro tipo de distribuciones si la única herramienta de la cual disponemos es una distribución uniforme pseudoaleatoria? Esto fue primeramente respondido por John von Neumann en la década de 1940 y se conoce como "Método de Muestreo de Aceptación/Rechazo".
Nota 1: Los perfeccionamientos al método de muestreo de Aceptación/Rechazo se conocen como:
-
Simulación Monte Carlo (von Neumann, Ulam & Metropolis, década de 1940)
- Método de muestreo estratificado Latino Hipercúbico (Iman, McKay & Eglājs, comienzos de 1980).
Nota 2 : En un muestreo estratifcado, la población total se divide en subgrupos o estratos y a continuación se seleccionan los representantes finales de cada estrato de un modo aleatorio y proporcional.
|
7.2 Histogramas y Funciones de Densidad de Probabilidad
Un Histograma corresponde a una representación gráfica de la distribución de cierta variable.
Por ejemplo, la tabla de un histograma del peso (en Kg) de cierto curso en un Colegio podría ser:
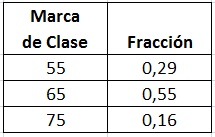
Y se lee:
Para un peso entre 50 y 60 Kg se encuentra el 29% de los miembros de la muestra.
Para un peso entre 60 y 70 Kg se encuentra el 55% de los miembros de la muestra.
Para un peso entre 70 y 80 Kg se encuentra el 16% de los miembros de la muestra.
El histograma de la distribución del peso será:
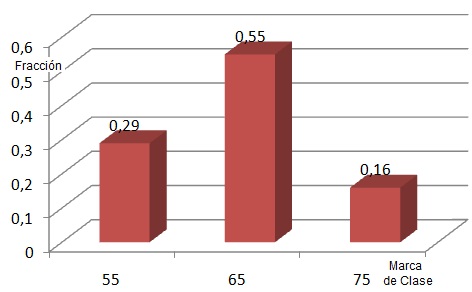
En este gráfico, el ancho de la base de cada columna es igual a 10 unidades. Cuando el ancho se hace tender a cero, el histograma se convierte en una "función densidad de probabildad" (fdp), teniendo ésto dos consecuencias:
1) El gráfico se puede expresar por medio de una función matemática
2) La probabilidad de que la variable aleatoria ubicada en el eje x se encuentre entre los valores a y b es igual al Area Bajo la Curva (ABC) de la fdp entre a y b.
Nota: El ABC es lo que técnicamente se conoce como "Integral".
7.3 Caso Especial: Función de densidad de probabilidad Normal o Gaussiana.
En Estadística las funciones de densidad de probabilidad (fdp) se utilizan para reflejar nuestro nivel de ignoracia sobre el valor específico de una variable, de modo que el máximo nivel de ignorancia matemáticamente viable es el siguiente:
-
Los valores posibles están dentro del intervalo a, b
- Todos los valores tienen la misma probabilidad.
La función matemática que representa esta situación se conoce como "fdp uniforme" y se expresa como:
f(x) = |
0 si x <a
1/(b-a) si a <= x <= b
0 si x >b |
Nota: Si las probabilidades presentan un sesgo, entonces nuestro nivel de ignorancia ya no es el máximo (de por sí, el sesgo es información extra).
Se puede tener un poco más de información cuando ocurre lo siguiente:
- Se conoce el valor más probable "MP"
- La probabilidad de obtener un valor mayor que MP es de 50% (la integral de la fdp entre MP e infinito es igual a 0.5)
- La probabilidad de obtener un valor menor que MP es de 50% (la integral de la fdp entre menos infinito y MP es igual a 0.5)
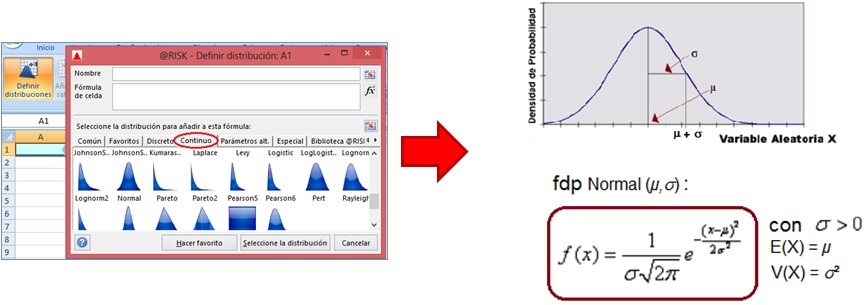
La fdp que refleja estas tres características se conoce como fdp "Normal" o Gaussiana y se encuentra en @Risk en la sección "Continuo" del botón "Definir distribución":
|
* La función que representa a la distribución normal en @Risk es: RiskNormal(E(x), V(x)), siendo E(x) la esperanza de x y V(x) la varianza de x.
*
La Metodología de Procesos Six Sigma modela el indicador de calidad correspondiente con una distribución Gaussiana o Normal y garantiza que en el peor de los casos se tendrá una no conformidad cada 3.4 millones de casos. Es decir, el intervalo donde se garantiza la calidad es de un ancho aproximado igual a 11 sigmas.
PASO 8: Instalación, configuración y descripción de @Risk
Para instalar la versión de prueba de @Risk, dé click en el link de Palisade Corporation que se proporciona abajo y complete el formulario con sus datos. Después de presionar el botón "Submit", usted recibirá en su correo electrónico un link de parte del Servicio al Cliente de Palisade que le permitirá descargar el archivo Risk[Versión]-Setup.exe. Una vez descargado el archivo, dé doble click sobre éste, seleccione "Español" para el idioma de instalación, acepte los términos del Contrato de Licencia e instale @Risk con la configuración por defecto, incluyendo un acceso directo en el Escritorio de Windows.
Al igual que XLSTAT, el programa quedará instalado como un complemento o Add-In de Excel, cuyo nombre será @Risk[Versión], teniendo como ubicación: "C:\Program Files\Palisade\Risk[Versión]\Risk.xla". La versión de prueba instalada será totalmente funcional durante 15 días y quedará disponible en la Cinta de Opciones de Excel bajo el encabezado "@Risk".
Nota 1: Si lo desea, puede descargar además SQL Server Express cuando el Asistente de Instalación se lo sugiera.
Nota 2: Los archivos de extensión "xla" corresponden a complementos escritos en Visual Basic for Applications (contienen macros y módulos).
Nota 3: Otra posible ubicación del Add-In es: C:\Program Files (x86)\Palisade\Risk[Versión]\Risk.xla (se agrega por medio de Archivo --> Opciones --> Complementos --> Ir)
Al dar doble click en el acceso directo a @Risk que se encuentra en el Escritorio, se activará Excel y podrá observar que en la cinta de opciones se encontrará la alternativa @Risk, incluyendo seis grupos en total:

Los grupos son: (1) @Risk, (2) Definir, (3) Simulación, (4) Resultados, (5) Herramientas, (6) Aplicación.
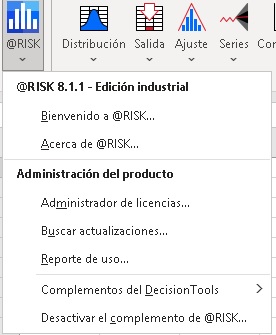
Grupo @Risk:
|
El grupo "@Risk" permite gestionar la utilización de la aplicación. Las opciones incluídas en este grupo son:
* Bienvenido, Acerca de
* Administrador de licencias, Buscar actualizaciones, Reporte de Uso
* Complementos del Decision Tools, Desactivar el complemento de @Risk
|
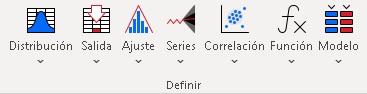
Grupo Definir:
|
El grupo "Definir" permite crear el modelo que relaciona los datos de entrada con los datos de salida para así realizar posteriormente la simulación Monte Carlo. Este grupo incluye:
* Distribución (fdp o funciones de densidad de probabilidad)
* Salida (output dependiente de entradas aleatorias)
* Ajuste de distribución empírica
* Series
* Definir correlaciones (en el caso de que existan variables aleatorias dependientes)
* Función
* Modelo |
Grupo Simulación:

|
El grupo "Simulacion" permite llevar a cabo el Método Monte Carlo. Por defecto se lanza una Simulación que incluye 100 iteraciones. En ciertas situaciones puede ser conveniente realizar más de una Simulación para así verificar que el resultado no depende de la semilla de los generadores de números pseudoaleatorios.
Este grupo incluye las opciones: Configurar, Iteraciones Simulaciones y Simular..
|
Grupo Resultados:
|
El grupo "Resultados" permite especificar el modo de visualización de los resultados de la ejecución del Método Monte Carlo. Las opciones de este grupo son: Explorar, Reportes, Visualizar Resultados, Resumen de Resultados y Definir Filtros.
|
Grupo Herramientas:
|
El grupo Herramientas incluye opciones de menú llamados:
* Optimizar
* Datos
* Utilidades |
Grupo Aplicación:

|
Este grupo incluye las siguientes opciones:
* Preferencias
* Ejemplos
* Recursos
* Colorear celdas, Base de conocimiento, Ayuda. |
PASO 9: En qué consiste el Muestreo Estratificado del Hipercubo Latino (Latin Hypercube Sampling, LHS)
En el contexto de la Estadística, un cuadrado latino es una grilla cuadrada que contiene las posiciones 2D de muestreo de modo que hay sólo una muestra en cada fila y en cada columna. Así mismo, un Hipercubo Latino es la generalización de este concepto a un número arbitrario de dimensiones, de modo que hay sólo una muestra en cada hiperplano posible que se alinea con el eje n-dimensional que lo contiene. LHS divide el rango de cada variable en N estratos equiprobables. Luego, para crear un Hipercubo Latino se necesitarán exactamente N puntos, lo que obliga a que todas las dimensiones estén dividida en exactamente N partes. Lo revelante en este esquema es que N no depende del número de coordenadas. Es decir, si las dimensiones aumentan N se mantendrá constante porque esa es la única forma de satisfacer la definición de Hipercubo Latino. Esta independencia del número de dimensiones es una de las ventajas obvias de LHS.
En el muestreo LH primero se debe decidir cuántos puntos de muestra utilizar y para cada punto de la muestra se debe recordar desde qué estrato n-dimensional proviene. En 2D dicha configuración es similar a tener N torres en un tablero de ajedrez, de modo que éstas no se amenazan entre sí y ojo que alinear muestras a lo largo de la diagonal no es la única forma de satisfacer este requisito. Debido a la estratificación, LHS asegura que el conjunto de números aleatorios seleccionado es representativo de la variabilidad real mientras que el muestreo aleatorio por fuerza bruta (Monte Carlo puro) no garantiza el muestreo de todos los estratos.
Paso 10: Qué es una Simulación Monte Carlo
10.1 Introducción al MMC
Los Métodos de Monte Carlo (o "Experimentos de Monte Carlo") corresponden a una clase de algoritmos computacionales que se basan en escoger repetidamente muestras que obedecen distribuciones probabilísticas predefinidas en el modelo inicial para así calcular resultados específicos. Los Métodos de Monte Carlo se utilizan a menudo en simulaciones por ordenador de sistemas que pueden ser representados matemáticamente. Estos métodos son adecuados para el cálculo mediante ordenador y tienden a ser utilizados cuando no es factible calcular un resultado exacto con un algoritmo totalmente determinista porque se desconoce el mecanismo de selección de las variables de entrada. Este método también se utiliza para complementar y justificar diversas teorías e hipótesis. Cuando los MMC se han aplicado en exploración espacial y prospección petrolera, sus predicciones de fallos, exceso de costos y atrasos posibles son significativamente superiores a la intuición humana o a alternativas conocidas como "métodos blandos”.
La versión moderna del MMC fue iniciado en la década de 1940 por Stanislaw Ulam mientras trabajaba en el proyecto de armas nucleares "Manhattan" en el Laboratorio Nacional de Los Alamos, Estados Unidos. Inmediatamente después del descubrimiento de Ulam, John von Neumann comprendió la importancia del algoritmo y programó la computadora ENIAC para realizar cálculos de Monte Carlo, siendo uno de los primeros cálculos la determinación del primer centenar de decimales del número pi.
Importante: El Método de Monte Carlo (MMC) se basa en obtener la caracterización estadística de las variables de salida de un modelo a partir de variables de entrada que obedecen ciertas fdps específicas. Según el método de Aceptación/Rechazo de von Neumann se puede obtener un muestreo basado en cualquier fdp a partir del generador de números pseudoaleatorios de cualquier computador. Esto se hace comparando las probabilidades uniformes generadas por el computador con la fdp correspondiente mediante un procedimiento estadístico especial, el cual se explica en detalle en la versión completa de este curso.
10.2 Ejemplo de construcción de un modelo que necesita apelar al MMC
Imaginemos un proyecto de inversión de capital que dura tres años y que presenta las siguientes características:
* Tasa de interés prevista: 7% anual
* Flujos de dinero a comienzos del primer año (n=0):
Ganancias previstas: 0.7 MUSD
Costos previstos: 1.3 MUSD
* Flujos de dinero a comienzos del segundo año (n=1):
Ganancias previstas: 0.8 MUSD
Costos previstos: 0,5 MUSD
* Flujos de dinero a comienzos del tercer año (n=2):
Ganancias previstas: 1.4 MUSD
Costos previstos: 0.4 MUSD
* Flujos de dinero al finalizar el tercer año (n=3):
Ganancias previstas: 0.9 MUSD
Costos previstos: 0,3 MUSD
El objetivo es calcular la rentabilidad del proyecto por medio del Valor Actualizado Neto:
VAN = sumatoria de los flujos netos por año llevados al presente por medio de la tasa de interés
El término n-ésimo de la sumatoria es:
Sn =
(Ganancia prevista - Costo previsto)n / (1 + interés)n
Si implementamos el modelo en Excel, obtendremos:
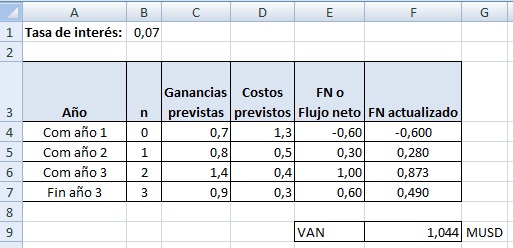
Resultados:
|
Fórmulas:
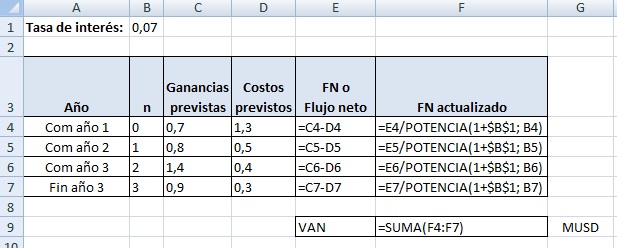
|
Por lo tanto el VAN de este proyecto después de tres años es de 1.044 MUSD, lo que lo vuelve rentable (VAN > 0).
SIn embargo el responsable de la evaluación económica, realiza las siguientes observaciones:
i) La tasa de interés diferencial no tiene por qué mantenerse constante e igual a 7% durante tres años. Es decir, existe una distribución de probabildad para la tasa de interés.
ii) Las ganancias son previstas y no seguras. Es decir, existe una distribución de probabildad para las ganancias.
iii) Los costos son previstos y no seguros. Es decir, existe una distribución de probabildad para los costos.
Lo anterior nos hace concluir que es imposible garantizar que el VAN del proyecto sea efectivamente igual a 1.044 MUSD.
Por lo tanto el responsable de la evaluación económica concluye que es mejor realizar una simulación MC formada por mil iteraciones, de modo que la decisión de invertir se base en el valor medio y desviación estándar del VAN, junto con el intervalo de confianza.
Paso 11: Ejemplo de una Simulación Monte Carlo en @Risk.
Para esta sección usaremos el modelo explicado en 10.2.
Imaginemos ahora que un Comité de Expertos estudió una base de datos conteniendo el desempeño de diversos proyectos y concluyó lo siguiente:
* La tasa de interés se distribuye de acuerdo con una fdp uniforme en el intervalo 0.05 a 0.11 (5% a 11%).
Luego, para la tasa de interés se debe utilizar RiskUniform(0,05; 0,11)
* Las ganancias previstas se distribuyen de acuerdo con una fdp normal, siendo mu igual al valor indicado en la sección 10.2 y sigma igual al 30% de mu.
Por ejemplo para la ganancia de n=0, mu vale 0.7 y sigma vale el 30% de 0.7, es decir, 0.21.
Luego, para las ganancia prevista para n=0 se debe utilizar RiskNormal(0,7; 0,21)
* Los costos previstos se distribuyen de acuerdo con una fdp PERT, de modo que el valor moda VM es el indicado en la sección 10.2, el valor mínimo es el 90% de VM y el valor máximo es el 120% de VM.
Por ejemplo, para el costo previsto de n=0, VM vale 1.3, el valor mínimo es 1.17 y el valor máximo es 1.56.
Luego, para el costo previsto de n=0 se debe utilizar RiskPert(1,17; 1,3; 1,56).
Considerando lo anterior, nuestros inputs quedarán así:

A continuación explicaremos como configurar los nueve inputs, desde el ítem (a) hasta el item (i).
a) Celda B1
- De click en B1
- De click en el botón Definir Distribución del grupo "Definir"
- Se activará la ventana "@Risk - Definir distribución"
- Vaya a la categoría "Continuas"
- De doble click en "Uniform"
|
- En la tabla de la izquierda, configure la distribución uniforme con mínimo = 0.05 y máximo = 0.11 (el valor estático 0.07 es el valor por defecto), tal como se indica en la siguiente figura:
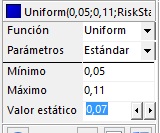
|
- Presione Aceptar
- En B1 podrá leer:
=RiskUniform(0,05;0,11;RiskStatic(0,07)) |
| . |
|
|
b) Celda C4
- De click en C4
- De click en el botón Definir Distribución del grupo "Definir"
- Se activará la ventana "@Risk - Definir distribución"
- Vaya a la categoría "Continuas"
- De doble click en "Normal" |
- En la tabla de la izquierda, configure la distribución nomal con mu = 0.7, sigma = 0.21 y el valor estático igual a 0.7, tal como se indica en la siguiente figura:
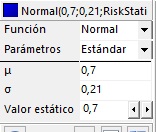
|
- Presione Aceptar
- En C4 podrá leer:
=RiskNormal(0,7;0,21;RiskStatic(0,7)) |
| . |
|
|
c) Celda C5
- De click en C5
- De click en el botón Definir Distribución del grupo "Definir"
- Se activará la ventana "@Risk - Definir distribución"
- Vaya a la categoría "Continuas"
- De doble click en "Normal" |
- En la tabla de la izquierda, configure la distribución nomal con mu = 0.8, sigma = 0.24 y el valor estático igual a 0.8, tal como se indica en la siguiente figura:
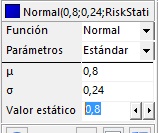
|
- Presione Aceptar
- En C5 podrá leer:
=RiskNormal(0,8;0,24;RiskStatic(0,8)) |
| x |
|
|
d) Celda C6
- De click en C6
- De click en el botón Definir Distribución del grupo "Definir"
- Se activará la ventana "@Risk - Definir distribución"
- Vaya a la categoría "Continuas"
- De doble click en "Normal" |
- En la tabla de la izquierda, configure la distribución nomal con mu = 1.4, sigma = 0.42 y el valor estático igual a 1.4, tal como se indica en la siguiente figura:
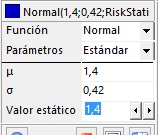
|
- Presione Aceptar
- En C6 podrá leer:
=RiskNormal(1,4;0,42;RiskStatic(1,4)) |
| x |
|
|
e) Celda C7
- De click en C7
- De click en el botón Definir Distribución del grupo "Definir"
- Se activará la ventana "@Risk - Definir distribución"
- Vaya a la categoría "Continuas"
- De doble click en "Normal" |
- En la tabla de la izquierda, configure la distribución nomal con mu = 0.9, sigma = 0.27 y el valor estático igual a 0.9, tal como se indica en la siguiente figura:
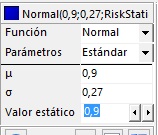
|
- Presione Aceptar
- En C7 podrá leer:
=RiskNormal(0,9;0,27;RiskStatic(0,9)) |
| x |
|
|
f) Celda D4
- De click en D4
- De click en el botón Definir Distribución del grupo "Definir"
- Se activará la ventana "@Risk - Definir distribución"
- Vaya a la categoría "Continuas"
- De doble click en "Pert" |
- En la tabla de la izquierda, configure la distribución PERT con mínimo=1.17, moda=1.3, máximo=1.56 y el valor estático igual a 1.3, tal como se indica en la siguiente figura:
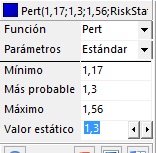
|
- Presione Aceptar
- En D4 podrá leer:
=RiskPert(1,17;1,3;1,56;RiskStatic(1,3))
|
| x |
|
|
g) Celda D5
- De click en D5
- De click en el botón Definir Distribución del grupo "Definir"
- Se activará la ventana "@Risk - Definir distribución"
- Vaya a la categoría "Continuas"
- De doble click en "Pert" |
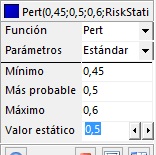
- En la tabla de la izquierda, configure la distribución PERT con mínimo=0.45, moda=0.5, máximo=0.6 y el valor estático igual a 0.5, tal como se indica en la siguiente figura:
|
- Presione Aceptar
- En D5 podrá leer:
=RiskPert(0,45;0,5;0,6;RiskStatic(0,5))
|
| x |
|
|
h) Celda D6
- De click en D6
- De click en el botón Definir Distribución del grupo "Definir"
- Se activará la ventana "@Risk - Definir distribución"
- Vaya a la categoría "Continuas"
- De doble click en "Pert" |
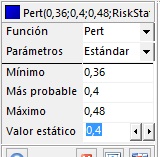
- En la tabla de la izquierda, configure la distribución PERT con mínimo=0.36, moda=0.4, máximo=0.48 y el valor estático igual a 0.4, tal como se indica en la siguiente figura:
|
- Presione Aceptar
- En D6 podrá leer:
=RiskPert(0,36;0,4;0,48;RiskStatic(0,4))
|
| x |
|
|
i) Celda D7
- De click en D7
- De click en el botón Definir Distribución del grupo "Definir"
- Se activará la ventana "@Risk - Definir distribución"
- Vaya a la categoría "Continuas"
- De doble click en "Pert" |
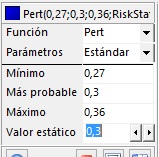
- En la tabla de la izquierda, configure la distribución PERT con mínimo=0.27, moda=0.3, máximo=0.36 y el valor estático igual a 0.3, tal como se indica en la siguiente figura:
|
- Presione Aceptar
- En D7 podrá leer:
=RiskPert(0,27;0,3;0,36;RiskStatic(0,3))
|
Ahora especificaremos que la celda F9 es el output de nuestra Simulación:
- Click en F9
- Click en el botón Salida → Definir. Aparecerá la siguiente ventana:

- Click en Aceptar
- En F9 podrá leerse la siguiente fórmula: =RiskOutput()+SUMA(F4:F7)
Este paso finaliza el diseño de nuestro Modelo.
A continuación ejecutaremos 3 simulaciones de 10 iteraciones cada una, de modo que cada iteración utilice una semilla distinta para el generador de números pseudoaleatorios.
* Primero se debe especificar que utilizaremos una semilla distinta para cada Simulación. Esto se realiza por medio de la siguiente secuencia: Click en el botón "Configurar" del grupo Simulación → Click en la ficha Muestreo → Seleccionar "Usar diferentes semillas" en la lista desplegable "Simulaciones Múltiples ".
* Configure Iteraciones en 10 y Simulaciones en 3:

* Para ver el avance de la Simulacón, posiciónese en una celda output. En este caso, de click en F9.
* Finalmente presione el botón "Simular" del grupo "Simulación".
* Después de un par de segundos, @Risk indicará que el proceso alcanzó el 100% y mostrará el histograma empírico de F9 obtenido en la Simulación por defecto (la primera).
Este paso finaliza la ejecución de las tres Simulaciones.
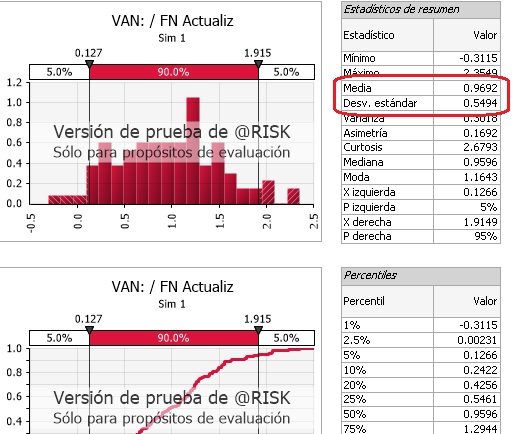
Ahora revisaremos uno de los informes más utilizados que nos permitirá caracterizar estadísticamente el comportamiento de nuestra celda output (F9):
- Click en el botón "Reportes" del grupo "Resultados"
- Click en "Reportes de Salida"
- Arriba escoja la opción "Compacto"
- De click en "Generar Reporte" (observe que en "Enviar a" se puede escoger la opción PDF)
Paso 12: Verificación de la Comprensión
1) ¿Qué se debe presionar en XLStat para que aprezca la siguiente ventana:
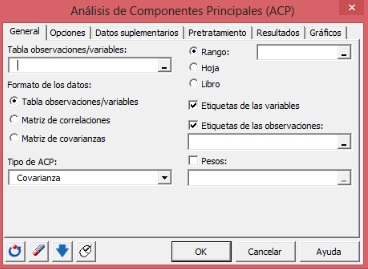 ? ?
|
.
2) Análisis de Componentes Principales
Una de las direcciones principales de la siguiente matriz
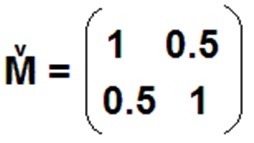
es:
|
.
3) @Risk
Imagine que en cierta aplicación de @Risk, se necesita realizar 20 simulaciones de 1000 iteraciones cada una.
¿Qué se debe hacer para que cada simulación genere muestreos distintos?
|
.
4) ¿Para qué se utiliza la función de Excel ALEATORIO.ENTRE(10, 15)?
|
.
Paso 13 : Cierre.
Felicitaciones. Usted ha llegado al final de este Taller donde conoció los fundamentos de dos poderosos complementos de Excel, a saber, XLSTAT y @Risk. Aprendió a llevar a cabo un Análisis de Componentes Principales en XLSTAT y a crear una Simulación Monte Carlo en @Risk. Lo alentamos a completar el cuestionario del Paso 14 para así obtener el certificado verificado de aprobación emitido por la empresa MT Trading, con un valor de USD 90. También le recordamos que puede inscribirse en el curso completo de 24 horas de XLSTAT y @Risk, ya sea en su versión web, con un valor de USD 210, o en la versión presencial por un valor de USD 370.
Paso 14 : Cuestionario
Utilice este formulario para enviarnos las respuestas.
Puntaje total del cuestionario: 20 puntos.
I) Preguntas por un punto cada una.
1) ¿Qué es un archivo "xlma"?
2) Respecto de la sección 6.2, ¿Cuánto vale el versor de Luis? (para el cálculo use los datos de B107:D107)
3) ¿Qué se debe presionar en XLStat para que la cinta de opciones aparezca en francés?
4) ¿En qué consiste el método de muestreo Latino Hipercúbico?
5) ¿Qué significa el término "Marca de Clase"?
6) ¿Qué datos presenta el Informe de @Risk "Datos de simulación (salidas)"?
7) Si se conoce la función de densidad de probabilidad de cierta variable u, ¿Cómo se calcula la probabilidad de que u esté ente a y b?
8) Respecto de la sección 10.2, ¿Cuánto vale el VAN si la tasa de interés (celda B1) toma el valor 3%?
II) Preguntas por 4 punto cada una.
9)
Encuentre los dos autovalores de la siguiente matriz de covarianzas:
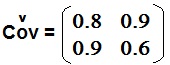
10) La fdp de cierta variable aleatoria x es:
| |
0 si x < 0 |
f(x): |
Ax si 0 <= x <= 3 |
| |
0 si x > 3 |
Encuentre el valor de A y justifique su respuesta.
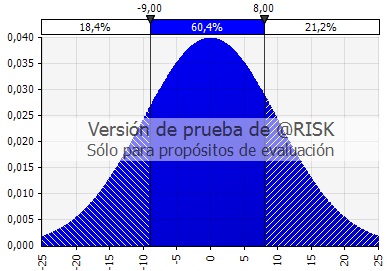
11) Para una fdp normal con mu=0 y sigma = 10, ¿Cuál es la probabilidad de que la variable aleatoria esté entre -11 y +11?
Obtenga un certificado verificado de aprobación extendido por la empresa MT Trading.

Para obtener el certificado de aprobación del Taller:
i) Envíenos sus respuestas al Cuestionario | Click aquí
ii) Si consigue un puntaje mínimo de 70%, le envíaremos el certificado impreso por medio de Correos de Chile (valor: USD 90).
|









































 ?
?